
【题目】如图,某处有一座信号塔AB,山坡BC的坡度为1:![]() ,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
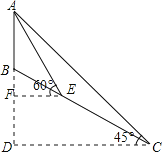
(1)求出山坡BC的坡角∠BCD的大小;
(2)求塔顶A到CD的铅直高度AD.(结果保留整数:![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
【答案】∠BCD=30°;(2)塔顶A到CD的铅直高度AD约为137米.
【解析】
(1)根据tan∠BCD=![]() ,进而得出答案;
,进而得出答案;
(2)设AD=x,则CD=AD=x,可得AF=x-50,EF=x-50![]() ,进而利用在Rt△AEF中,
,进而利用在Rt△AEF中,![]() =tan60°,求出答案.
=tan60°,求出答案.
(1)依题意得:tan∠BCD=![]() =
=![]() ,
,
∴∠BCD=30°;
(2)作EG⊥CD,垂足为G.

在Rt△CEG中,CE=100,∠ECG=30°,
∴EG=CEsin30°=50,
CG=CEcos30°=50![]() ,
,
设AD=x,则CD=AD=x.
∴AF=x-50,EF=x-50![]() ,
,
在Rt△AEF中,![]() =tan60°,
=tan60°,
∴![]() .
.
解得:x=50![]() +50≈136.5(米).
+50≈136.5(米).
答:塔顶A到CD的铅直高度AD约为137米.


科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
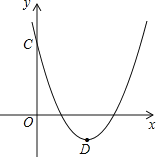
(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;
(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;
(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为______.
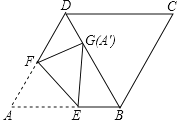
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象记作
的图象记作![]() ,一次函数
,一次函数![]() 的图象记作
的图象记作![]() ,对于这两个图象,有以下几种说法:
,对于这两个图象,有以下几种说法:
①当![]() 与
与![]() 有公共点时,
有公共点时,![]() 随
随![]() 增大而减小;
增大而减小;
②当![]() 与
与![]() 没有公共点时,
没有公共点时,![]() 随
随![]() 增大而增大;
增大而增大;
③当![]() 时,
时,![]() 与
与![]() 平行,且平行线之间的距离为
平行,且平行线之间的距离为![]() .
.
下列选项中,描述准确的是( )
A. ①②正确,③错误B. ①③正确,②错误
C. ②③正确,①错误D. ①②③都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
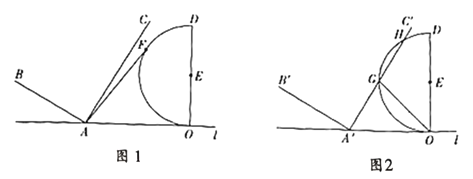
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为________;
的最大值为________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图,若![]() 截半圆
截半圆![]() 的
的![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
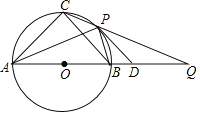
【题目】如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为![]() 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论:①若∠PAB=30°,则
上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论:①若∠PAB=30°,则![]() 的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6
的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6![]() ;④无论点P在
;④无论点P在![]() 上的位置如何变化,CPCQ为定值.其中正确的是________________.(写出所有正确结论的序号)
上的位置如何变化,CPCQ为定值.其中正确的是________________.(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com