
【题目】如图,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
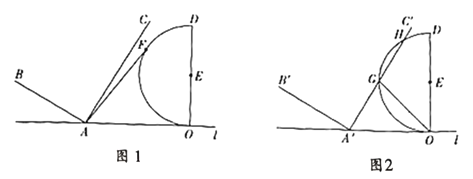
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为________;
的最大值为________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图,若![]() 截半圆
截半圆![]() 的
的![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)由图可知当点F与点D重合时,AF最大,根据勾股定理即可求出此时AF的长;
(2)①连接EG、EH.根据![]() 的长为π可求得∠GEH=60°,可得△GEH是等边三角形,根据等边三角形的三个角都等于60°得出∠HGE=60°,可得EG//A'O,求得∠GEO=90°,得出△GEO是等腰直角三角形,求得∠EGO=45°,根据平角的定义即可求出∠A'GO的度数;
的长为π可求得∠GEH=60°,可得△GEH是等边三角形,根据等边三角形的三个角都等于60°得出∠HGE=60°,可得EG//A'O,求得∠GEO=90°,得出△GEO是等腰直角三角形,求得∠EGO=45°,根据平角的定义即可求出∠A'GO的度数;
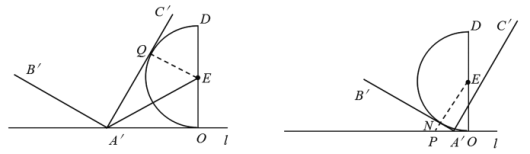
②分C'A'与半圆相切和B'A'与半圆相切两种情况进行讨论,利用切线的性质、勾股定理、切斜长定理等知识进行解答即可得出答案.
解:
(1)当点F与点D重合时,AF最大,
AF最大=AD=![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)①连接![]() 、
、![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
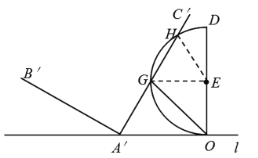
②当![]() 切半圆
切半圆![]() 于
于![]() 时,连接
时,连接![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() 切半圆
切半圆![]() 于
于![]() 点,
点,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴平移距离为![]() .
.
当![]() 切半圆
切半圆![]() 于
于![]() 时,连接
时,连接![]() 并延长
并延长![]() 于
于![]() 点,
点,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是40元,根据市场调查:在一段时间内,销售单价是50元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>50),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | ① |
销售玩具获得利润ω(元) | ② |
(2)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于54元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
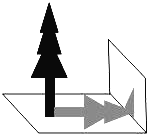
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.5m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1m,又测得地面的影长为1.5m,请你帮她算一下,树高为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某处有一座信号塔AB,山坡BC的坡度为1:![]() ,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
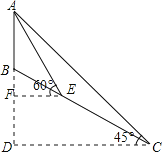
(1)求出山坡BC的坡角∠BCD的大小;
(2)求塔顶A到CD的铅直高度AD.(结果保留整数:![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李宁准备完成题目;解二元一次方程组![]() ,发现系数“□”印刷不清楚.
,发现系数“□”印刷不清楚.
(1)他把“□”猜成3,请你解二元一次方程组![]() ;
;
(2)张老师说:“你猜错了”,我看到该题标准答案的结果x、y是一对相反数,通过计算说明原题中“□”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
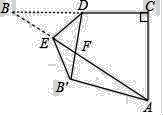
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年五一期间采石矶景区将启用新的大门,景区决定利用现有的不同种类花卉设计出两种不同的造型A和B摆放于大门广场.已知每个A种造型的成本y1与造型个数x(0<x<60)满足关系式y1=82﹣![]() x,每个B种造型的成本y2与造型个数x(0<x<60)的关系如表所示:
x,每个B种造型的成本y2与造型个数x(0<x<60)的关系如表所示:
x(个) | … | 10 | 20 | 30 | 50 | … |
y2(元) | … | 93 | 86 | 79 | 65 | … |
(1)请求出y2与x的函数关系式;
(2)现在广场需搭配A、B两种园艺造型共60个,要求每种园艺造型不得少于20个,并且成本总额W(元)不超过5000元.以上要求能否同时满足?请你通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
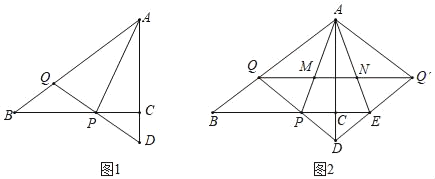
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点P在线段BC上,点Q在线段AB上,且PQ=BQ,延长QP交射线AC于点D.
(1)求证:QA=QD;
(2)设∠BAP=α,当2tanα是正整数时,求PC的长;
(3)作点Q关于AC的对称点Q′,连结QQ′,AQ′,DQ′,延长BC交线段DQ′于点E,连结AE,QQ′分别与AP,AE交于点M,N(如图2所示).若存在常数k,满足kMN=PEQQ′,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com