
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
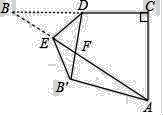
【答案】3或![]()
【解析】
△AB′F为直角三角形,应分两种情况进行讨论.当∠AFB′为直角时,利用勾股定理求出B′E,也就是BE的长,便求出AE。当∠AB′F为直角时,过A作AN⊥EB′,交EB′的延长线于N,构造Rt△B′EF,利用勾股定理便可求出AE.
解:①当B′D⊥AE时,△AB′F为直角三角形,如下图:
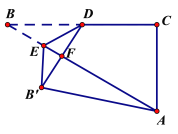
根据题意,BE=B′E,BD= B′D=![]() BC=
BC=![]() . ∠B=∠EB′F
. ∠B=∠EB′F
∵在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2
,AC=2
∴AB=![]() =
=![]() =4
=4
∴∠B=∠EB′F =30°.
∵在Rt△BDF中,∠B=30°
∴DF=![]() BD=
BD=![]()
∴B′F=B′D-DF=![]() -
-![]() =
=![]()
∵在Rt△B′EF中,∠EB′F =30°
∴EF=![]() B′E,
B′E,
∵B′F=![]() =
=![]() =
=![]() EF,
EF,
即![]() =
=![]() EF,
EF,
∴EF=![]() ,则BE=1,
,则BE=1,
∴AE=AB-BE=4-1=3.
②当D B′⊥A B′时,△AB′F为直角三角形,如下图:
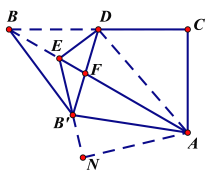
连接AD,过A作AN⊥EB′,交EB′的延长线于N.
根据题意,BE=B′E,BD=CD=B′D=![]() BC=
BC=![]() . ∠B=∠EB′F
. ∠B=∠EB′F
∵在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2
,AC=2
∴AB=![]() =
=![]() =4
=4
∴∠B=∠EB′F =30°.
∵∠AB′F=90°
∴∠AB′E=∠AB′F+∠EB′F=120°
∴Rt△AB′N中,∠AB′N=60°,∠B′AN=30°
∴B′N=![]() AB′
AB′
在Rt△AB′D和Rt△ACD中
![]()
∴Rt△AB′D≌Rt△ACD(HL)
∴AB′=AC=2
∴B′N=1,AN=![]()
设AE=x,则BE= B′E=4-x
∵在Rt△AEN中,![]()
∴(![]() )2+(4-x+1)2=x2
)2+(4-x+1)2=x2
∴x=![]()
综上,AE的长为3或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() . 将线段
. 将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,
,![]() 是边
是边![]() 上的一动点,连接
上的一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)点![]() 在边
在边![]() 上,且
上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
①判断![]() 与
与![]() 的位置关系,并证明你的结论;②连接
的位置关系,并证明你的结论;②连接![]() ,若
,若![]() ,请直接写出线段
,请直接写出线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
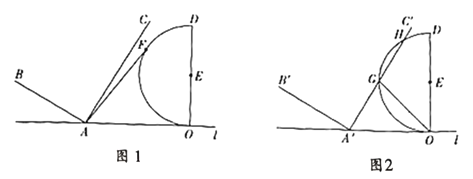
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为________;
的最大值为________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图,若![]() 截半圆
截半圆![]() 的
的![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
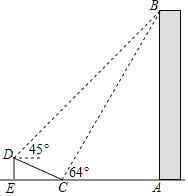
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
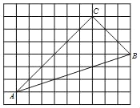
【题目】如图,在边长为1个单位长度的小正方形组成的8×10网格中,点A,B,C均为网格线的交点.
(1)用无刻度的直尺作BC边上的中线AD(不写作法,保留作图痕迹);
(2)①在给定的网格中,以A为位似中心将△ABC缩小为原来的![]() ,得到△AB'C',请画出△AB'C'.
,得到△AB'C',请画出△AB'C'.
②填空:tan∠AB'C'= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对初三学生进行物理、化学实验操作能力测试.物理、化学各有3个不同的操作实验题目,物理实验分别用①、②、③表示,化学实验分别用a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.王刚同学对物理的①、②号实验和化学的b、c号实验准备得较好.请用画树状图(或列表)的方法,求王刚同学同时抽到两科都准备得较好的实验题目的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com