
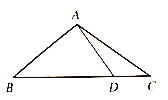
【题目】如图,在![]() 中,
中,![]() ,点D在
,点D在![]() 边上,且
边上,且![]() ,将
,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,点B的对应点为E,
,点B的对应点为E,![]() 与边
与边![]() 交于点F,则
交于点F,则![]() 的长为_____________.
的长为_____________.
【答案】![]()
【解析】
过A作AH⊥BC于H,由等腰三角形的性质得出BH=CH,∠B=∠C,由tanB=
![]() =
=![]() ,设AH=
,设AH=![]() x,则BH=3x,在Rt△ABH中,由勾股定理得出方程,求出BH=CH=3,DH=CH-CD=2,BD=BH+DH=5,由折叠可得,BD=DE,∠E=∠ABC=∠C,AB=AE=4,证明△AFE∽△DFC,得出
x,则BH=3x,在Rt△ABH中,由勾股定理得出方程,求出BH=CH=3,DH=CH-CD=2,BD=BH+DH=5,由折叠可得,BD=DE,∠E=∠ABC=∠C,AB=AE=4,证明△AFE∽△DFC,得出![]() =
=![]() =
=![]() =
=![]() , 设CF=a,则EF=4a,AF=4-a,得出DF=
, 设CF=a,则EF=4a,AF=4-a,得出DF=![]() , 由DF+EF=DE=5得出方程,求出a的值,即可得出EF的长.
, 由DF+EF=DE=5得出方程,求出a的值,即可得出EF的长.
解:如图所示,过A作AH⊥BC于H,
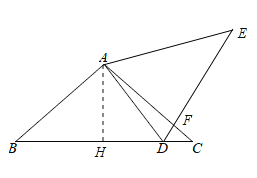
∵AB=AC=4,∴BH=CH,∠B=∠C,
∵tanB=![]() =
=![]() ,
,
设AH=![]() x,则BH=3x,在Rt△ABH中,由勾股定理得:
x,则BH=3x,在Rt△ABH中,由勾股定理得:
(3x)2+(![]() x)2=42,
x)2=42,
解得:x=1,
∴BH=CH=3,
∴DH=CH-CD=2,
∴BD=BH+DH=5,
由折叠可得,BD=DE,∠E=∠ABC=∠C,AB=AE=4,
又∵∠AFE=∠DFC,
∴△AFE∽△DFC,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
设CF=a,则EF=4a,AF=4-a,
∴DF=![]() AF=1-
AF=1-![]() a,
a,
∵DF+EF=DE=5,
∴4a+1-![]() a=5,
a=5,
解得:a=![]() ,
,
∴EF=4×![]() =
=![]() ,
,
故答案为:![]()


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
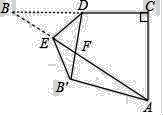
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒) | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
(1)计算表中a,b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100kg麦种,则有多少千克的麦种可以成活为秧苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
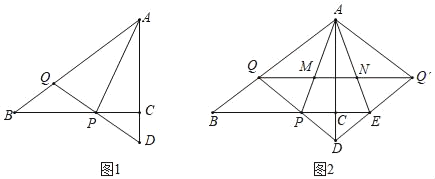
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点P在线段BC上,点Q在线段AB上,且PQ=BQ,延长QP交射线AC于点D.
(1)求证:QA=QD;
(2)设∠BAP=α,当2tanα是正整数时,求PC的长;
(3)作点Q关于AC的对称点Q′,连结QQ′,AQ′,DQ′,延长BC交线段DQ′于点E,连结AE,QQ′分别与AP,AE交于点M,N(如图2所示).若存在常数k,满足kMN=PEQQ′,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.
(1)求购买1个排球、1个篮球的费用分别是多少元?
(2)若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字分别是1,2,3,4 的四张扑克牌背面朝上,洗匀后放在桌面上.

(1)从中随机抽出一张牌,牌面数字是偶数的概率是_____;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是 4 的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
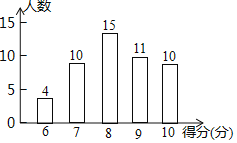
【题目】为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,并用得到的数据绘制了如图条形统计图(得分为整数,满分为10分,最低分为6分)
请根据图中信息,解答下列问题:
(1)本次调查一共抽取了 名居民;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”,请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 与
与![]() 的平分线相交于点P,
的平分线相交于点P,![]() ,PB与CE交于点H,
,PB与CE交于点H,![]() 交BC于F,交AB于G,下列结论:①
交BC于F,交AB于G,下列结论:①![]() ;②
;②![]() ;③ BP垂直平分CE;④
;③ BP垂直平分CE;④![]() ,其中正确的判断有( )
,其中正确的判断有( )
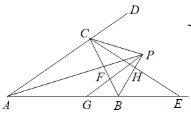
A. ①②B. ③④C. ①③④D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com