
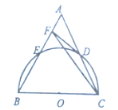
【题目】如图,以等边![]() 的边
的边![]() 为直径画半圆,分别交边
为直径画半圆,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() 是半圆的切线,交
是半圆的切线,交![]() 于点
于点![]() ,若
,若![]() 的长为1,则
的长为1,则![]() 的面积为( )
的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接OD,由DF为圆的切线,利用切线的性质得到OD垂直于DF,根据三角形ABC为等边三角形,利用等边三角形的性质得到三条边相等,三内角相等,都为60°,由OD=OC,得到三角形OCD为等边三角形,进而得到OD平行与AB,由O为BC的中点,得到D为AC的中点,在直角三角形ADF中,利用30°所对的直角边等于斜边的一半求出AD的长,进而求出AC的长,即为AB的长,由AB-AF求出FB的长,在直角三角形FBG中,利用30°所对的直角边等于斜边的一半求出BG的长,再利用三角函数即可求出FG的长.最后用三角形的面积公式即可.
如图,连接OD,过点F作FG⊥BC,
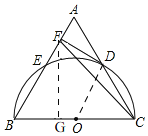
∵DF为圆O的切线,
∴OD⊥DF,
∵△ABC为等边三角形,
∴AB=BC=AC,∠A=∠B=∠ACB=60°,
∵OD=OC,
∴△OCD为等边三角形,
∴∠CDO=∠A=60°,∠ABC=∠DOC=60°,
∴OD∥AB,
∴DF⊥AB,
在Rt△AFD中,∠ADF=30°,AF=1,
∴AD=2AF=2,
∴AC=4,即:BC=AC=4,
∴FB=AB-AF=4-1=3,
在Rt△BFG中,∠BFG=30°,
∴cos∠BFG=![]() ,
,
∴FG=![]() BF=
BF=![]() .
.
∴S△FBC=![]() BC×FG=
BC×FG=![]() ×4×
×4×![]() =3
=3![]() ,
,
故选A.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于点
分别与x轴、y轴交于点![]() 和点B,直线
和点B,直线![]() 分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为
分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为![]() 的中点。
的中点。
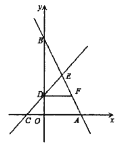
(1)求直线![]() 的解析式;
的解析式;
(2)过点D作![]() 轴,交直线
轴,交直线![]() 于点F,求
于点F,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.5m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1m,又测得地面的影长为1.5m,请你帮她算一下,树高为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某处有一座信号塔AB,山坡BC的坡度为1:![]() ,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
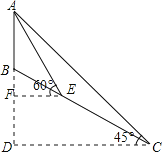
(1)求出山坡BC的坡角∠BCD的大小;
(2)求塔顶A到CD的铅直高度AD.(结果保留整数:![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李宁准备完成题目;解二元一次方程组![]() ,发现系数“□”印刷不清楚.
,发现系数“□”印刷不清楚.
(1)他把“□”猜成3,请你解二元一次方程组![]() ;
;
(2)张老师说:“你猜错了”,我看到该题标准答案的结果x、y是一对相反数,通过计算说明原题中“□”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
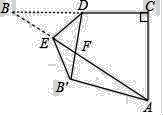
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒) | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
(1)计算表中a,b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100kg麦种,则有多少千克的麦种可以成活为秧苗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com