
【题目】如图,直线![]() 与坐标轴相交于A、B两点,点P为x轴正半轴上的一个动点,当△PAB是等腰三角形时,点P的坐标为_____.
与坐标轴相交于A、B两点,点P为x轴正半轴上的一个动点,当△PAB是等腰三角形时,点P的坐标为_____.
【答案】(![]() ,0)或(9,0).
,0)或(9,0).
【解析】
利用一次函数图象上点的坐标特征可求出点A,B的坐标,利用勾股定理可求出AB的长,分PA=PB和AB=AP两种情况考虑:①当PA=PB时,设点P的坐标为(m,0),利用PA=PB可得出关于m的方程,解之即可得出点P的坐标;②当AB=AP时,由AB=5可得出AP=5,结合OA=4可得出OP的长,进而可得出点P的坐标.综上,此题得解.
解:当x=0时,y=﹣![]() x+3=3,
x+3=3,
∴OB=3,点B的坐标为(0,3);
当y=0时,﹣![]() x+3=0,解得:x=4,
x+3=0,解得:x=4,
∴OA=4,点A的坐标为(4,0).
∴AB=![]() =5
=5
分两种情况考虑,如图所示.
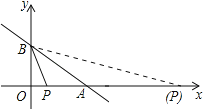
①当PA=PB时,设点P的坐标为(m,0),则PA=4﹣m,PB=![]() ,
,
∴4﹣m=![]() ,
,
解得:m=![]() ,
,
∴点P的坐标为(![]() ,0);
,0);
②当AB=AP时,AP=5,
∴OP=OA+AP=9,
∴点P的坐标为(9,0).
故答案为:(![]() ,0)或(9,0).
,0)或(9,0).


科目:初中数学 来源: 题型:
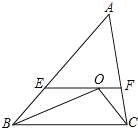
【题目】如图,△ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC交AB、AC于E、F,若△ABC的周长比△AEF的周长大12cm,O到AB的距离为4cm,△OBC的面积_____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是直线y=x+4与坐标轴的交点,直线y=-2x+b过点B,与x轴交于点C.
(1)求A,B,C三点的坐标;
(2)点D是折线A—B—C上一动点.
①当点D是AB的中点时,在x轴上找一点E,使ED+EB的和最小,用直尺和圆规画出点E的位置(保留作图痕迹,不要求写作法和证明),并求E点的坐标.
②是否存在点D,使△ACD为直角三角形,若存在,直接写出D点的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
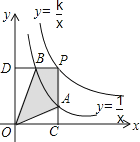
【题目】反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴,交y=
的图象上,PC⊥x轴,交y=![]() 的图象于点A,PD⊥y轴,交y=
的图象于点A,PD⊥y轴,交y=![]() 的图象于点B.当点P在y=
的图象于点B.当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于平面直角坐标系xOy中的点P(a,b)和直线y=ax+b,我们称点P((a,b)是直线y=ax+b的关联点,直线y=ax+b是点P(a,b)的关联直线.特别地,当a=0时,直线y=b(b为常数)的关联点为P(0,b).
如图,已知点A(-2,-2),B(4,-2),C(1,4).
(1)点A的关联直线的解析式为______;
直线AB的关联点的坐标为______;
(2)设直线AC的关联点为点D,直线BC的关联点为点E,点P在y轴上,且S△DEP=2,求点P的坐标.
(3)点M(m,n)是折线段AC→CB(包含端点A,B)上的一个动点.直线l是点M的关联直线,当直线l与△ABC恰有两个公共点时,直接写出m的取值范围.
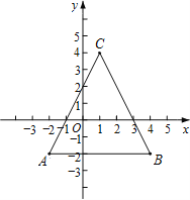
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com