
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
ШчЭМЂйЃЌЁїABCКЭЁїAEDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=ЁЯEAD=90ЁуЃЌЕуBдкЯпЖЮAEЩЯЃЌЕуCдкЯпЖЮADЩЯЃЌЧыжБНгаДГіЯпЖЮBEгыЯпЖЮCDЕФЪ§СПЙиЯЕЃК ЃЛ
ЃЈ2ЃЉВйзїЬНОП
ШчЭМЂкЃЌНЋЭМЂйжаЕФЁїABCШЦЕуAЫГЪБеыа§зЊЃЌа§зЊНЧЮЊІСЃЈ0Ёу![]() ІС
ІС![]() 360ЁуЃЉЃЌЧыХаЖЯВЂжЄУїЯпЖЮBEгыЯпЖЮCDЕФЪ§СПЙиЯЕЃЛ
360ЁуЃЉЃЌЧыХаЖЯВЂжЄУїЯпЖЮBEгыЯпЖЮCDЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉНтОіЮЪЬт
НЋЭМЂйжаЕФЁїABCШЦЕуAЫГЪБеыа§зЊЃЌа§зЊНЧЮЊІСЃЈ0Ёу![]() ІС
ІС![]() 360ЁуЃЉЃЌШєDE=2ACЃЌдка§зЊЕФЙ§ГЬжаЃЌЕБвдAЁЂBЁЂCЁЂDЫФЕуЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧыжБНгаДГіа§зЊНЧІСЕФЖШЪ§ ЃЎ
360ЁуЃЉЃЌШєDE=2ACЃЌдка§зЊЕФЙ§ГЬжаЃЌЕБвдAЁЂBЁЂCЁЂDЫФЕуЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧыжБНгаДГіа§зЊНЧІСЕФЖШЪ§ ЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉ45ЁуЃЌ225ЁуЛђ315Ёу
ЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉ45ЁуЃЌ225ЁуЛђ315Ёу
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУABЃНACЃЌAEЃНADЃЌдйИљОнЕШСПЙиЯЕПЩЕУЯпЖЮBEгыЯпЖЮCDЕФЙиЯЕЃЛ
ЃЈ2ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУABЃНACЃЌAEЃНADЃЌИљОна§зЊЕФаджЪПЩЕУЁЯBAEЃНЁЯCADЃЌИљОнSASПЩжЄЁїBAEЁеЁїCADЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЧѓНтЃЛ
ЃЈ3ЃЉИљОнЦНааЫФБпаЮЕФаджЪПЩЕУЁЯABCЃНЁЯADCЃН45ЁуЃЌдйИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁпЁїABCКЭЁїAEDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBACЃНЁЯEADЃН90ЁуЃЌ
ЁрABЃНACЃЌAEЃНADЃЌ
ЁрAEABЃНADACЃЌ
ЁрBEЃНCDЃЌ
ЙЪД№АИЮЊЃКBEЃНCDЃЛ
ЃЈ2ЃЉЁпЁїABCКЭЁїAEDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBACЃНЁЯEADЃН90ЁуЃЌ
ЁрABЃНACЃЌAEЃНADЃЌ
гЩа§зЊЕФаджЪЕУЃЌЁЯBAEЃНЁЯCADЃЌ
дкЁїBAEгыЁїCADжа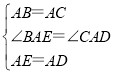 ЃЌ
ЃЌ
ЁрЁїBAEЁеЁїCADЃЈSASЃЉ
ЁрBEЃНCDЃЛ
ЃЈ3ЃЉШчЭМЃЌ
ЁпвдAЁЂBЁЂCЁЂDЫФЕуЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЁїABCКЭЁїAEDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯABCЃНЁЯADCЃН45ЁуЃЌ
ЁпEDЃН2ACЃЌ
ЁрACЃНCDЃЌ
ЁрЂйЕБCЕуа§зЊгкC1ЮЛжУЪБЁЯCADЃН45ЁуЃЌ
ЂкЕБCЕуа§зЊгкC2ЮЛжУЪБЁЯCADЃН360Ёу90Ёу45ЁуЃН225ЁуЃЌ
ЂлЕБCЕуа§зЊгкC3ЮЛжУЪБЁЯCADЃН360Ёу45ЁуЃН315ЁуЃЌ
ЁрНЧІСЕФЖШЪ§ЪЧ45ЁуЛђ225ЁуЛђ315ЁуЃЌ
ЙЪД№АИЮЊЃК45ЁуЛђ225ЁуЛђ315ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌвд
ЃЌвд![]() ЮЊжБОЖЕФдВ
ЮЊжБОЖЕФдВ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌгы
ЃЌгы![]() ЕФбгГЄЯпЯрНЛгкЕу
ЕФбгГЄЯпЯрНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]()
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧдВ
ЪЧдВ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдНвАздааГЕЪЧжабЇЩњЯВАЎЕФНЛЭЈЙЄОпЃЌЪаГЁОоДѓЃЌОЙељвВМЄСв.ФГЦЗХЦОЯњЩЬОгЊЕФ![]() аЭГЕШЅФъЯњЪлзмЖюЮЊ
аЭГЕШЅФъЯњЪлзмЖюЮЊ![]() ЭђдЊЃЌНёФъУПСОЪлМлБШШЅФъНЕЕЭ
ЭђдЊЃЌНёФъУПСОЪлМлБШШЅФъНЕЕЭ![]() дЊЃЌШєТєГіЕФЪ§СПЯрЭЌЃЌЯњЪлзмЖюНЋБШШЅФъМѕЩй
дЊЃЌШєТєГіЕФЪ§СПЯрЭЌЃЌЯњЪлзмЖюНЋБШШЅФъМѕЩй![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЩшНёФъ![]() аЭГЕУПСОЯњЪлМлЮЊ
аЭГЕУПСОЯњЪлМлЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉИУЦЗХЦОЯњЩЬМЦЛЎаТНјвЛХњ![]() аЭГЕКЭаТПю
аЭГЕКЭаТПю![]() аЭГЕЙВ
аЭГЕЙВ![]() СОЃЌЧв
СОЃЌЧв![]() аЭГЕЕФНјЛѕЪ§СПВЛГЌЙ§
аЭГЕЕФНјЛѕЪ§СПВЛГЌЙ§![]() аЭГЕЪ§СПЕФСНБЖЃЌЧыЮЪгІШчКЮАВХХСНжжаЭКХГЕЕФНјЛѕЪ§СПЃЌВХФмЪЙетХњЪлГіКѓЛёРћзюЖрЃП
аЭГЕЪ§СПЕФСНБЖЃЌЧыЮЪгІШчКЮАВХХСНжжаЭКХГЕЕФНјЛѕЪ§СПЃЌВХФмЪЙетХњЪлГіКѓЛёРћзюЖрЃП
![]() ЁЂ
ЁЂ![]() СНжжаЭКХГЕНёФъЕФНјЛѕКЭЯњЪлМлИёБэ
СНжжаЭКХГЕНёФъЕФНјЛѕКЭЯњЪлМлИёБэ
|
| |
НјЛѕМл |
|
|
ЯњЪлМл |
|
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
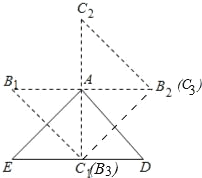
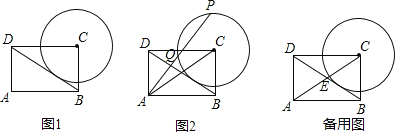
ЁОЬтФПЁПвбжЊдкОиаЮABCDжаЃЌABЃН4ЃЌADЃН3ЃЌЁбCгыЖдНЧЯпBDЯрЧаЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓЁбCЕФАыОЖЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуPЪЧЁбCЩЯвЛИіЖЏЕуЃЌСЌНгAPЃЌACЃЌAPНЛЁбCгкЕуQЃЌШєsinЁЯPACЃН![]() ЃЌЧѓЁЯCPAЕФЖШЪ§КЭЛЁPQЕФГЄЃЛ
ЃЌЧѓЁЯCPAЕФЖШЪ§КЭЛЁPQЕФГЄЃЛ
ЃЈ3ЃЉШчЭМЃЌЖдНЧЯпACгыЁбCНЛгкЕуEЃЌЕуPЪЧЁбCЩЯвЛИіЖЏЕуЃЌЩшЕуPЕНжБЯпACЕФОрРыЮЊdЃЌЕБ0ЃМdЁм![]() ЪБЃЌЧыжБНгаДГіЁЯPCEЖШЪ§ЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌЧыжБНгаДГіЁЯPCEЖШЪ§ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЅЕуЮЊDЕФХзЮяЯпyЃНЉx2+bx+cНЛxжсгкAЁЂB(3ЃЌ0)ЃЌНЛyжсгкЕуCЃЌжБЯпyЃНЉ![]() x+mОЙ§ЕуCЃЌНЛxжсгкE(4ЃЌ0)ЃЎ
x+mОЙ§ЕуCЃЌНЛxжсгкE(4ЃЌ0)ЃЎ
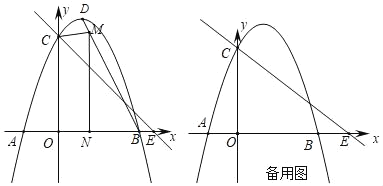
(1)ЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
(2)ШчЭМ1ЃЌЕуMЮЊЯпЖЮBDЩЯВЛгыBЁЂDжиКЯЕФвЛИіЖЏЕуЃЌЙ§ЕуMзїxжсЕФДЙЯпЃЌДЙзуЮЊNЃЌЩшЕуMЕФКсзјБъЮЊxЃЌЫФБпаЮOCMNЕФУцЛ§ЮЊSЃЌЧѓSгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓSЕФзюДѓжЕЃЛ
(3)ЕуPЮЊxжсЕФе§АыжсЩЯвЛИіЖЏЕуЃЌЙ§PзїxжсЕФДЙЯпЃЌНЛжБЯпyЃНЉ![]() x+mгкGЃЌНЛХзЮяЯпгкHЃЌСЌНгCHЃЌНЋЁїCGHбиCHЗелЃЌШєЕуGЕФЖдгІЕуFЧЁКУТфдкyжсЩЯЪБЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
x+mгкGЃЌНЛХзЮяЯпгкHЃЌСЌНгCHЃЌНЋЁїCGHбиCHЗелЃЌШєЕуGЕФЖдгІЕуFЧЁКУТфдкyжсЩЯЪБЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАаЃдАвєРжжЎЩљЁАНсЪјКѓЃЌЭѕРЯЪІећРэСЫЫљгаВЮШќбЁЪжЕФБШШќГЩМЈЃЈЕЅЮЛЃКЗжЃЉЃЌЛцжЦГЩШчЯТЦЕЪ§жБЗНЭМКЭЩШаЮЭГМЦЭМЃК
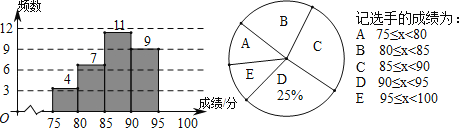
ЃЈ1ЃЉЧѓБОДЮБШШќВЮШќбЁЪжзмШЫЪ§ЃЌВЂВЙШЋЦЕЪ§жБЗНЭМЃЛ
ЃЈ2ЃЉЧѓЩШаЮЭГМЦЭМжаЩШаЮEЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ3ЃЉГЩМЈдкEЧјгђЕФбЁЪжжаЃЌФаЩњБШХЎЩњЖрвЛШЫЃЌДгжаЫцЛњбЁШЁСНШЫЃЌЧѓЧЁКУбЁжаСНУћХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЩЭжаЛЊЪЋДЪЃЌбАЮФЛЏЛљвђЃЌЦЗЩњЛюжЎУРЁБЃЌФГаЃОйАьСЫЪзНьЁАжаЙњЪЋДЪДѓЛсЁБЃЌОбЁАЮКѓга50УћбЇЩњВЮМгОіШќЃЌИљОнВтЪдГЩМЈЃЈГЩМЈЖМВЛЕЭгк50ЗжЃЉЛцжЦГіШчЭМЫљЪОЕФВПЗжЦЕЪ§ЗжВМжБЗНЭМЃЎ
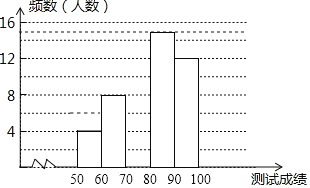
ЧыИљОнЭМжааХЯЂЭъГЩЯТСаИїЬтЃЎ
ЃЈ1ЃЉНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећШЫЪ§ЃЛ
ЃЈ2ЃЉШєВтЪдГЩМЈВЛЕЭгк80ЗжЮЊгХауЃЌдђБОДЮВтЪдЕФгХауТЪЪЧЖрЩйЃЛ
ЃЈ3ЃЉЯжНЋДгАќРЈаЁУїКЭаЁЧПдкФкЕФ4УћГЩМЈгХвьЕФЭЌбЇжаЫцЛњбЁШЁСНУћВЮМгЪаМЖБШШќЃЌЧѓаЁУїгыаЁЧПЭЌЪББЛбЁжаЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕуGдкБп
ЃЌЕуGдкБп![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌзї
ЃЌзї![]() гкЕуEЃЌ
гкЕуEЃЌ![]() гкЕуFЃЌСЌНг
гкЕуFЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
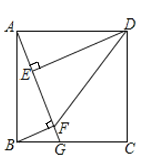
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєЕуGДгЕуBби![]() БпдЫЖЏжСЕуCЭЃжЙЃЌЧѓЕуEЃЌFЫљОЙ§ЕФТЗОЖгыБп
БпдЫЖЏжСЕуCЭЃжЙЃЌЧѓЕуEЃЌFЫљОЙ§ЕФТЗОЖгыБп![]() ЮЇГЩЕФЭМаЮЕФУцЛ§ЃЎ
ЮЇГЩЕФЭМаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=![]() x2+bx+cОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌЦфжаЕуAЃЈ0ЃЌ1ЃЉЃЌЕуBЃЈЉ9ЃЌ10ЃЉЃЌACЁЮxжсЃЌЕуPЪБжБЯпACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЎ
x2+bx+cОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌЦфжаЕуAЃЈ0ЃЌ1ЃЉЃЌЕуBЃЈЉ9ЃЌ10ЃЉЃЌACЁЮxжсЃЌЕуPЪБжБЯпACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛЃЈ2ЃЉЙ§ЕуPЧвгыyжсЦНааЕФжБЯпlгыжБЯпABЁЂACЗжБ№НЛгкЕуEЁЂFЃЌЕБЫФБпаЮAECPЕФУцЛ§зюДѓЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕБЕуPЮЊХзЮяЯпЕФЖЅЕуЪБЃЌдкжБЯпACЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУвдCЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃЌШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com