
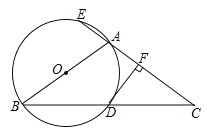
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 的延长线相交于点
的延长线相交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
((1)由等腰三角形的性质可证∠ODB=∠C,从而OD//AC,可证OD⊥DF,即可解决问题;
(2)连结BE,根据直径所对的圆周角为直角得出![]() ,根据已知用AE表示出AB、EC、BE,从而可得
,根据已知用AE表示出AB、EC、BE,从而可得![]() ,然后由△DFC∽△BEC,得
,然后由△DFC∽△BEC,得![]() ,由此即可计算CF长.
,由此即可计算CF长.
(1)证明:如图,连接OD,
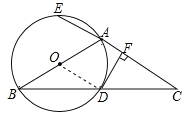
∵OB=OD,∴∠B=∠ODB.
∵AB=AC,∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线
(2)解:如图,连接BE,
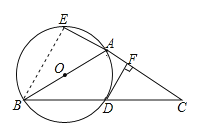
∵AB是直径,
∴∠AEB=90°.
∵AB=AC,AC=3AE,
∴AB=3AE,CE=4AE,
∴BE=![]() =
=![]() AE,
AE,
∴![]() .
.
∵∠DFC=∠AEB=90°,
∴DF∥BE,
∴△DFC∽△BEC,
∴![]() ,
,
∴DF=![]() FC.
FC.
∵DF=2,
∴CF=![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
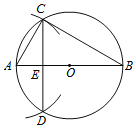
【题目】已知⊙O.如图,
(1)作⊙O的直径AB;
(2)以点A为圆心,AO长为半径画弧,交⊙O于C,D两点;
(3)连接CD交AB于点E,连接AC,BC.
根据以上作图过程及所作图形,有下面三个推断:
①CE=DE; ②BE=3AE; ③BC=2CE.
所有正确推断的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药,12周后,记录了两组患者的生理指标![]() 和
和![]() 的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
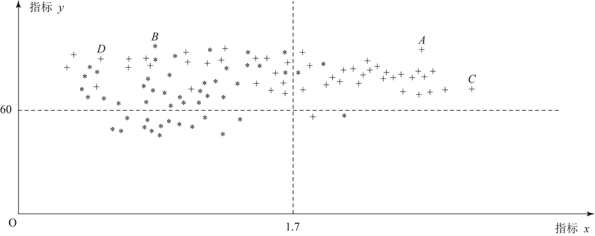
同时记录了服药患者在4周、8周、12周后的指标z的改善情况,并绘制成条形统计图.

根据以上信息,回答下列问题:
(1)从服药的50名患者中随机选出一人,求此人指标![]() 的值大于1.7的概率;
的值大于1.7的概率;
(2)设这100名患者中服药者指标![]() 数据的方差为
数据的方差为![]() ,未服药者指标
,未服药者指标![]() 数据的方差为
数据的方差为![]() ,则
,则![]()
![]() ;(填“>”、“=”或“<” )
;(填“>”、“=”或“<” )
(3)对于指标z的改善情况,下列推断合理的是 .
①服药4周后,超过一半的患者指标z没有改善,说明此药对指标z没有太大作用;
②在服药的12周内,随着服药时间的增长,对指标z的改善效果越来越明显.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象如图,现给出下列结论:①
的图象如图,现给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 的两个根为
的两个根为![]() ,
,![]() ,其中正确的结论有( )
,其中正确的结论有( )
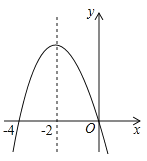
A.①③④B.②④⑤C.①②⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,点
,点![]() ,
,![]() 分别对应点
分别对应点![]() ,
,![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 三点在同一条直线上,连接
三点在同一条直线上,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 的外接圆圆O与
的外接圆圆O与![]() 交于
交于![]() 、
、![]()
(1)求证:![]() 是圆O切线;
是圆O切线;
(2)如图2连接![]() ,
,![]() ,若
,若![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长.
的长.
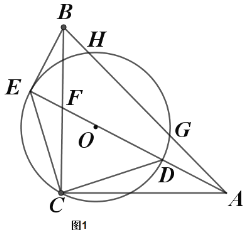

查看答案和解析>>
科目:初中数学 来源: 题型:
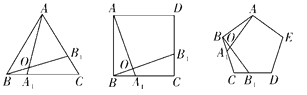
【题目】如图,下列正多边形都满足BA1=CB1,在正三角形中,我们可推得:∠AOB1=60°;在正方形中,可推得:∠AOB1=90°;在正五边形中,可推得:∠AOB1=108°,依此类推在正八边形中,AOB1=____°,在正n(n≥3)边形中,∠AOB1=____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
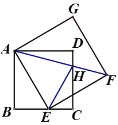
【题目】如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFG,对角线AF交边CD于H,连EH.①BE+DH=EH;②若E为BC的中点,则H为CD的中点;③EF平分∠HEC;④![]() .其中正确的序号是_______.
.其中正确的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究
如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0°![]() α
α![]() 360°),请判断并证明线段BE与线段CD的数量关系;
360°),请判断并证明线段BE与线段CD的数量关系;
(3)解决问题
将图①中的△ABC绕点A顺时针旋转,旋转角为α(0°![]() α
α![]() 360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数 .
360°),若DE=2AC,在旋转的过程中,当以A、B、C、D四点为顶点的四边形是平行四边形时,请直接写出旋转角α的度数 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com