
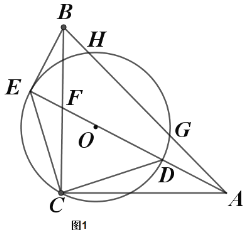
【题目】如图1,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,点
,点![]() ,
,![]() 分别对应点
分别对应点![]() ,
,![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 三点在同一条直线上,连接
三点在同一条直线上,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 的外接圆圆O与
的外接圆圆O与![]() 交于
交于![]() 、
、![]()
(1)求证:![]() 是圆O切线;
是圆O切线;
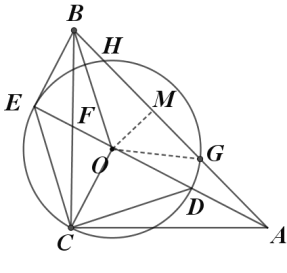
(2)如图2连接![]() ,
,![]() ,若
,若![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)平行四边形,见解析(3)![]()
【解析】
(1)利用旋转的性质可得:![]() ,
,![]() 由三角形内角和可得
由三角形内角和可得![]() =90°,即可证明
=90°,即可证明![]() 是圆O切线;
是圆O切线;
(2)由等腰三角形的性质可得:![]() ,可得:
,可得:![]() ,可得
,可得![]()
由![]() ,可设
,可设![]() ,
,![]() 可得
可得![]() ,故
,故![]() ,由
,由![]() ,可得
,可得![]() ,可得
,可得![]() ,即可判断四边形
,即可判断四边形![]() 的形状;
的形状;
(3)计算得![]() ,
,![]()
根据勾股定理列出方程:![]() ,求出x的值,即可求出
,求出x的值,即可求出![]() ,
,![]() ,运用相似三角形的判定可得:
,运用相似三角形的判定可得:![]() ,利用相似三角形的性质可求出
,利用相似三角形的性质可求出 ![]() ,根据勾股定理渴求出MG的长度,即可求出GH的长度;
,根据勾股定理渴求出MG的长度,即可求出GH的长度;
(1)证明:由旋转可知![]() ,
,![]()
![]() 是⊙O的直径
是⊙O的直径
∵![]()
又∵![]()
∴![]()
![]()
![]()
又∵OE是⊙O的半径
![]() 是⊙O的切线
是⊙O的切线
(2)四边形![]() 是平行四边形
是平行四边形
理由如下:
由旋转可知,![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]() 在
在![]() 中
中
![]()
在![]() 中
中
设![]() ,
,![]()
![]()
![]()
![]()
![]()
由旋转可知:![]()
![]()
又∵![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
(3)![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
![]() 由旋转可知:
由旋转可知:![]()
在![]() 中
中
![]()
![]() 在
在![]() 中
中
![]()
![]()
解得,![]()
![]() ,
,![]()
如图,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 中
中
![]()
![]()
![]() (取正值)
(取正值)
![]()


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.折一折:把边长为![]() 的正方形纸片
的正方形纸片![]() 对折,使边
对折,使边![]() 与
与![]() 重合,展开后得到折痕
重合,展开后得到折痕![]() .如图①:点
.如图①:点![]() 为
为![]() 上一点,将正方形纸片
上一点,将正方形纸片![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,展开后连接
处,展开后连接![]() ,
,![]() ,
,![]() ,如图②
,如图②
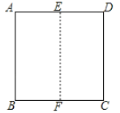
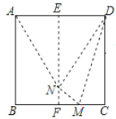
图① 图②
(一)填一填,做一做:
(1)图②中,![]() _______.线段
_______.线段![]() _______.
_______.
(2)图②中,试判断![]() 的形状,并给出证明.
的形状,并给出证明.
剪一剪、折一折:将图②中的![]() 剪下来,将其沿直线
剪下来,将其沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,分别得到图③、图④.
处,分别得到图③、图④.
(二)填一填
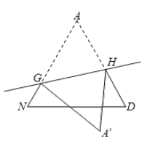
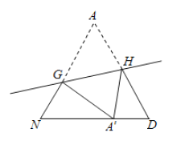
图③ 图④
(3)图③中阴影部分的周长为_______.
(4)图③中,若![]() ,则
,则![]() _______°.
_______°.
(5)图③中的相似三角形(包括全等三角形)共有_______对;
(6)如图④点![]() 落在边
落在边![]() 上,若
上,若![]() _______,则
_______,则![]() _______用含
_______用含![]() ,
,![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=![]() ,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转
,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转![]() 角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
小宇发现点E的位置,![]() 和
和![]() 的大小都不确定,于是他从特殊情况开始进行探究.
的大小都不确定,于是他从特殊情况开始进行探究.
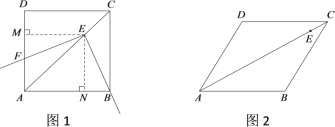
(1)如图1,当![]() =
=![]() =90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得
=90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得![]() ,并由全等三角形的性质得到EB与EF的数量关系为 .
,并由全等三角形的性质得到EB与EF的数量关系为 .
(2)如图2,当![]() =60°,
=60°,![]() =120°时,
=120°时,
①依题意补全图形;
②请帮小宇继续探究(1)的结论是否成立.若成立,请给出证明;若不成立,请举出反例说明;
(3)小宇在利用特殊图形得到了一些结论之后,在此基础上对一般的图形进行了探究,设∠ABE=![]() ,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角
,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角![]() ,
,![]() ,
,![]() 满足的关系: .
满足的关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
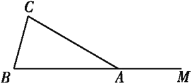
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1)按下列要求作图,并在图中标明相应的字母.(保留作图痕迹)
①作∠MAC的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD;
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
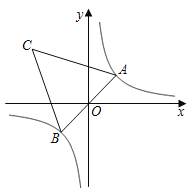
【题目】如图,在反比例函数![]() 的图象上有一动点
的图象上有一动点![]() ,连接
,连接![]() 并延长交图象的另一支于点
并延长交图象的另一支于点![]() ,在第二象限内有一点
,在第二象限内有一点![]() ,满足
,满足![]() ,当点
,当点![]() 运动时,点
运动时,点![]() 始终在函数
始终在函数![]() 的图象上运动,若
的图象上运动,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
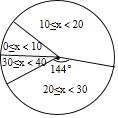
【题目】“校园音乐之声“结束后,王老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如下频数直方图和扇形统计图:
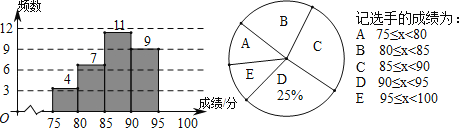
(1)求本次比赛参赛选手总人数,并补全频数直方图;
(2)求扇形统计图中扇形E的圆心角度数;
(3)成绩在E区域的选手中,男生比女生多一人,从中随机选取两人,求恰好选中两名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com