
����Ŀ��ʱ����ѧ��ѧ����Ȥ������ʵʩ��������߰���.Ϊ���˽�ѧ����ϲ����һ�������˶����Ա�������Ż���أ���ȫУ����ϲ��һ�����ࣨƹ������ë���������������˶���1200��ѧ���У������ȡ��������ѧ�����е��飨ÿ��ֻ���������������˶���ѡ��һ�֣�.������ͳ�����£�
�������� | ƹ���� | ��ë�� | ���� | ���� | ���� |
���� | 42 |
| 15 | 33 |
|
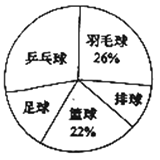
����������⣺
��1����γ��������е�������________��
��2��ͳ�Ʊ��У�![]() ________��
________��![]() ________��
________��
��3���Թ�������1200��ѧ������ϲ��ƹ�����˶�������.
���𰸡���1��ʱ����ѧѧ����ϲ����һ�������˶��������2��39��21����3��336��.
������������: ��1��ֱ�����������Ķ�������ó��𰸣�
��2����ϲ�������������������ռ�İٷֱȼ��������������������������������ë����ռ�İٷֱȼ������a��������������ȥ�������bֵ��
��3��������������ϲ��ƹ���������ռ�İٷֱȼ���.
���:
��1����γ��������е������ǣ�ʱ����ѧѧ����ϲ����һ�������˶������
�ʴ�Ϊ��ʱ����ѧѧ����ϲ����һ�������˶������
��2����ϲ���������33�ˣ�ռ22%��
����������Ϊ33��22%=150��
a=150��26%=39���ˣ���
b=150-39-42-15-33=21���ˣ���
�ʴ�Ϊ��39��21��
��3����ϲ��ƹ�����˶�������Ϊ��1200��![]() =336���ˣ���
=336���ˣ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
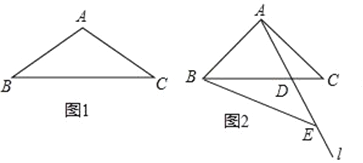
����Ŀ���۽�������ABC�У���BAC��90�㣬AB=AC����ACB=��������A��ֱ��l��BC���ڵ�D����E��ֱ��l�ϣ���BC=BE������E��AD�ӳ����ϣ�
�ٵ���=30������Dǡ��ΪBC�е�ʱ����ȫͼ1ֱ��д����BAE=���㣬
��BEA=���㣻
����ͼ2������BAE=2�������BEA�Ķ������ú����Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
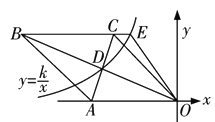
����Ŀ����ͼ������OABC��һ��OA��x��ĸ������ϣ�O������ԭ�㣬A������Ϊ����10,0�����Խ���AC��OB�ཻ�ڵ�D��AC��OB=160.������������y=![]() (x��0����ͼ����D������BC���ӳ��߽��ڵ�E,��S��OCE��S��OAB=________.
(x��0����ͼ����D������BC���ӳ��߽��ڵ�E,��S��OCE��S��OAB=________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O(0��0)��B(1��2)��
��1������A��y���ϣ���������AOB�����Ϊ2�����A�����ꣻ
��2������C������Ϊ(3��0)��BD��OC����BD��OC�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC������OA��OC�ֱ���x���y���ϣ�����OA=5��OC=3�����Ѿ���OABC���ŵ�O��ʱ����ת��ʹ��Aǡ������BC���ϵ�A1�������C�Ķ�Ӧ��C1������Ϊ��������
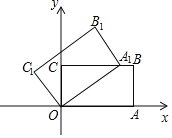
A. ����![]() �� B. ����
�� B. ����![]() �� C. ����
�� C. ����![]() �� D. ����
�� D. ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
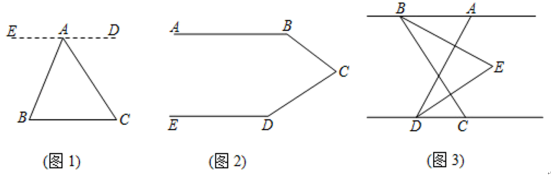
����Ŀ���Ƚ�ת������ͼ1����֪��A��BC��һ�㣬����AB��AC�����BAC+��B+��C�Ķ�����
��1���Ķ��������������������
�⣺����A��ED��BC��
���B����EAB����C���� ������ ����
�֡ߡ�EAB+��BAC+��DAC��180��
���B+��BAC+��C��180��
����������������У����Ƿ���ƽ���߾������Ƚ�ת�����Ĺ��ܣ�����BAC����B����C��������һ�𣬵ó���֮��Ĺ�ϵ��ʹ������Խ����
��2����ͼ2����֪AB��ED�����B+��BCD+��D�Ķ�������ʾ������C��CF��AB����
��3����ͼ3����֪AB��CD����C�ڵ�D���Ҳ࣬��ADC��80������B�ڵ�A����࣬��ABC��60����BEƽ�֡�ABC��DEƽ�֡�ADC��BE��DE���ڵ�ֱ�߽��ڵ�E����E������ƽ����AB��CD֮�䣬���BED�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
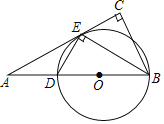
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬BEƽ�֡�ABC��AC�ڵ�E����ED��EB��AB�ڵ�D����O����BED�����Բ��
��1����֤��AC�ǡ�O�����ߣ�
��2����֪��O�İ뾶Ϊ2.5��BE=4����BC��AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�O��AC��һ���㣬����O��ֱ��MN��BC����MN����BCA��ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F.����O�˶���AC���е㣬���ACB=_____��ʱ���ı���AECF�������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ���˽����̰༶ѧ���κ�ϰ�ľ���������Ա��ಿ��ѧ��������һ���µĸ��ٵ��飬Ȼ�������ֳ����ࣺA�����㣻B�����ã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ��
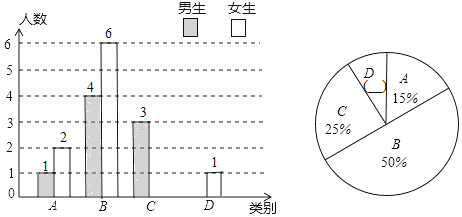
�����ͳ��ͼ����������⣺
��1�����ε����У�����ʦһ���������� ����ѧ��������C��Ů������ ������D���������� ������
��2����ȫ���������ͳ��ͼ������ͳ��ͼ��
��3���ڴ˴ε����У�Сƽ����D�࣮Ϊ�˽�������������ʦ�ӱ������A��ѧ�������ѡȡһλͬѧ������������һ��һ���Ŀκ���ѧϰ���������ѡ��ͬѧǡ����һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com