Question

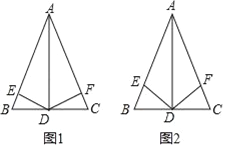
【题目】（1）如图1：在△ABC中，AB=AC，AD⊥BC，DE⊥AB于点E，DF⊥AC于点F．证明：DE=DF．

（2）如图2，在△ABC中，AB=AC，AD⊥BC，DE和DF分别平分∠ADB和∠ADC，求证：DE=DF．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）在△ABC中，AB=AC，AD⊥BC，根据等腰三角形三线合一的性质可得∠BAD=∠CAD，又因DE⊥AB，DF⊥AC，根据角平分线的性质定理即可证得DE=DF；（2）在△ABC中，AB=AC，AD⊥BC，根据等腰三角形三线合一的性质可得∠BAD=∠CAD，∠ABD=∠CDA=90°，又因DE平分∠ADB，DF平分和∠ADC，可得∠ADE=∠ADF=45°，利用ASA证得△AED≌△AFD，根据全等三角形等的性质即可得结论.

试题解析：

（1）证明：∵AB=AC，AD⊥BC，

∴∠BAD=∠CAD，

∵DE⊥AB，DF⊥AC

∴DE=DF；

（2）证明：∵AB=AC，AD⊥BC

∴∠BAD=∠CAD，

∵DE平分∠ADB，DF平分和∠ADC，

∴∠ADE=∠ADF=45°，

在△AED和△AFD中，

，

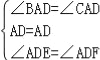∴△AED≌△AFD（ASA），

∴DE=DF．