
 如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC与BD交于点0,∠AOB=60°,P、Q、R分别是OA、BC、OD的中点.求证:△PQR是正三角形.
如图所示,在等腰梯形ABCD中,AB∥CD,AD=BC,AC与BD交于点0,∠AOB=60°,P、Q、R分别是OA、BC、OD的中点.求证:△PQR是正三角形. 分析 由于梯形ABCD是等腰梯形∠AOB=60°,可知△OCD与△OAB均为等边三角形.连接CR,BP根据等边三角形的性质可知△BCR与△BPC为直角三角形,再利用直角三角形的性质可知QR=BP=$\frac{1}{2}$BC,由中位线定理可知,QR=QP=PS=$\frac{1}{2}$BC,故△PQR是等边三角形.
解答 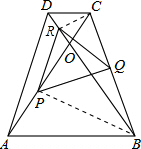 证明:连结CR,BP.
证明:连结CR,BP.
∵四边形ABCD是等腰梯形,且AC与BD相交于O,
∴可得出:△CAB≌△DBA,
∴∠CAB=∠DBA,
同理可得出:∠ACD=∠BDC,
∴AO=BO,CO=DO.
∵∠ACD=60°,
∴△OCD与△OAB均为等边三角形.
∵R是OD的中点,
∴CR⊥DO.
在Rt△BRC中,Q为BC中点,RQ是斜边BC的中线,
∴RQ=$\frac{1}{2}$BC.
同理BP⊥AC.
在Rt△BPC中,PQ=$\frac{1}{2}$BC.
又∵RP是△OAD的中位线,
∴RP=$\frac{1}{2}$AD=$\frac{1}{2}$BC.
∴RP=PQ=SQ.
∴△PQR为等边三角形.
点评 本题主要考查等腰梯形及直角三角形的性质,三角形中位线定理等知识,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
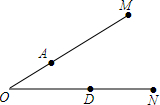 如图,角形铁架∠M0N小于60°,A,D分别是0M,0N上的点,为实际设计的需要,需在OM和0N上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
如图,角形铁架∠M0N小于60°,A,D分别是0M,0N上的点,为实际设计的需要,需在OM和0N上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
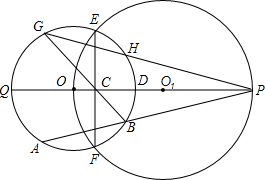 如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:
如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com