
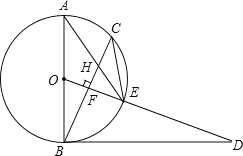
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA=![]() ,求BH的长.
,求BH的长.
【答案】(1)证明见解析;
(2)证明见解析;
(3)BH=![]() .
.
【解析】
试题分析:(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;
(2)连接AC,由垂径定理得出![]() ,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论;
,即可得出结论;
(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.
试题解析:(1)∵∠ODB=∠AEC,∠AEC=∠ABC,∴∠ODB=∠ABC,
∵OF⊥BC,∴∠BFD=90°,∴∠ODB+∠DBF=90°,∴∠ABC+∠DBF=90°,
即∠OBD=90°,∴BD⊥OB,∴BD是⊙O的切线;
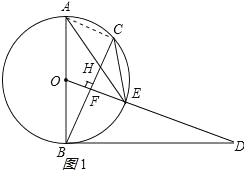
(2)连接AC,如图1所示:∵OF⊥BC,∴![]() ,
,
∴∠CAE=∠ECB,∵∠CEA=∠HEC,∴△CEH∽△AEC,
∴![]() ,
,
∴CE2=EHEA;
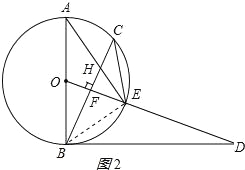
(3)连接BE,如图2所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE=![]() ,
,
∴AB=10,BE=ABsin∠BAE=10×![]() =6,
=6,
∴EA=![]() =8,
=8,
∵![]() ,∴BE=CE=6,∵CE2=EHEA,
,∴BE=CE=6,∵CE2=EHEA,
∴EH=![]() ,
,
在Rt△BEH中,BH=![]() =
= =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
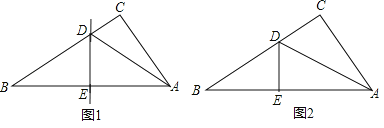
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是新中国成立70周年,是决胜全面建成小康社会第一个百年奋斗目标的关键之年,脱贫攻坚成效明显.按照现行农村贫困标准计算,2019年末农村贫困人口比上年末减少1109万人,将1109万人用科学记数法表示为________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)判断下列事件中,哪些是确定事件,哪些是不确定事件?
①丙抢到金额为1元的红包;
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多;
(2)记金额最多、居中、最少的红包分别为A,B,C.
①求出甲抢到红包A的概率;
②若甲没抢到红包A,则乙能抢到红包A的概率又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
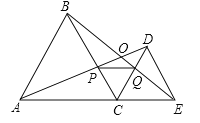
①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com