
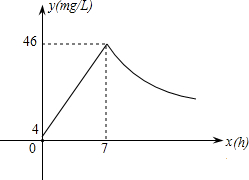 ���������ҹ�ú��ȫ�¹�ƵƵ����������Σ����������˹������Ҫ�ɷ���CO����һ�ο����¼��ĵ����з��֣�����ʱ�𣬾��ڿ�����CO��Ũ�ȴﵽ4mg/L���˺�Ũ�ȳ�ֱ�������ӣ��ڵ�7Сʱ�ﵽ���ֵ46mg/L��������ը����ը�����е�COŨ�ȳɷ������½�����ͼ���������������Ϣ�ش��������⣺
���������ҹ�ú��ȫ�¹�ƵƵ����������Σ����������˹������Ҫ�ɷ���CO����һ�ο����¼��ĵ����з��֣�����ʱ�𣬾��ڿ�����CO��Ũ�ȴﵽ4mg/L���˺�Ũ�ȳ�ֱ�������ӣ��ڵ�7Сʱ�ﵽ���ֵ46mg/L��������ը����ը�����е�COŨ�ȳɷ������½�����ͼ���������������Ϣ�ش��������⣺���� ��1�����ô���ϵ�������һ�κ����Ľ���ʽ�ͷ����������Ľ���ʽ��
��2�����y=4ʱ����Ӧ�ķ����������ĺ���ֵ��Ȼ���ȥ7������⣮
��� �⣺��1����Ϊ��ըǰŨ�ȳ�ֱ�������ӣ����Կ���y��x�ĺ�����ϵʽΪy=k1x+b��
��ͼ��֪y=k1x+b��
���㣨0��4���루7��46����
��$\left\{\begin{array}{l}{b=4}\\{7{k}_{1}+b=46}\end{array}\right.$�����$\left\{\begin{array}{l}{{k}_{1}=6}\\{b=4}\end{array}\right.$��
����y=6x+4����ʱ�Ա���x��ȡֵ��Χ��0��x��7��
��Ϊ��ը��Ũ�ȳɷ������½������Կ���y��x�ĺ�����ϵʽΪy=$\frac{{k}_{2}}{x}$��
��ͼ��֪y=$\frac{{k}_{2}}{x}$��
���㣨7��46������$\frac{{k}_{2}}{7}$=46��
���k2=322��
����y=$\frac{322}{x}$����ʱ�Ա���x��ȡֵ��Χ��x��7��
��2����y=4ʱ����y=$\frac{322}{x}$�ã�x=80.5��80.5-7=73.5��Сʱ����
�ʿ������ڱ�ը��73.5Сʱ�����¾���
���� ���⿼���˷�����������ʵ��Ӧ�ã���ʵ�����д��ڴ����ɷ�������������������������������Ĺؼ���ȷ����������֮��ĺ�����ϵ��Ȼ�����ô���ϵ����������ǵĹ�ϵʽ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
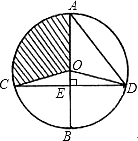 ��ͼ����O��ֱ��AB����CD������ΪE������AD��OC��OD����OD=5��
��ͼ����O��ֱ��AB����CD������ΪE������AD��OC��OD����OD=5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
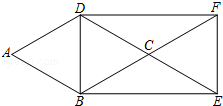 ��ͼ������ABCD�У��ֱ��ӳ�DC��BC����E��F��ʹCE=CD��CF=CB������DB��BE��EF��FD��
��ͼ������ABCD�У��ֱ��ӳ�DC��BC����E��F��ʹCE=CD��CF=CB������DB��BE��EF��FD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
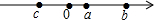 �����ϱ�ʾa��b��c�������ĵ��λ����ͼ��ʾ�������н�����ȷ���ǣ�������
�����ϱ�ʾa��b��c�������ĵ��λ����ͼ��ʾ�������н�����ȷ���ǣ�������| A�� | abc��0 | B�� | c-b��a | C�� | b+c��0 | D�� | |a+c|��|b| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ�����ص��������գ��մ������գ�C�������ݣ�J�������أ�����C•J�������4����λ�϶�������ʱ�������Թ����Ƶ��������ǣ�������
��ͼ��һ�����ص��������գ��մ������գ�C�������ݣ�J�������أ�����C•J�������4����λ�϶�������ʱ�������Թ����Ƶ��������ǣ�������| A�� | 1000�� | B�� | 10000�� | C�� | 9999�� | D�� | 9000�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�С�ABC�͡�ACBƽ���߽��ڵ�O������O��OD��BC�ڵ�D����ABC���ܳ�Ϊ18��OD=4�����ABC�������36��
��ͼ���ڡ�ABC�С�ABC�͡�ACBƽ���߽��ڵ�O������O��OD��BC�ڵ�D����ABC���ܳ�Ϊ18��OD=4�����ABC�������36���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com