
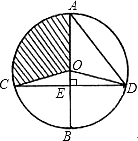
 如图,⊙O的直径AB⊥弦CD,垂足为E,连接AD、OC、OD,且OD=5.
如图,⊙O的直径AB⊥弦CD,垂足为E,连接AD、OC、OD,且OD=5.分析 (1)由垂径定理得出DE=$\frac{1}{2}$CD=4,由勾股定理求出OE,得出AE,再由勾股定理求出AD即可;
(2)设∠ADO=4x,则∠EDO=x,由等腰三角形的性质得出∠OAD=∠ADO=4x,由直角三角形的性质得出方程,解方程求出∠ADC=50°,由圆周角定理得出∠AOC=100°,由扇形面积公式即可得出结果.
解答 解:(1)∵直径AB⊥弦CD,
∴DE=$\frac{1}{2}$CD=4,
由勾股定理得:OE=$\sqrt{O{D}^{2}-D{E}^{2}}$=3,
∴AE=5+3=8,
∴AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=4$\sqrt{5}$;
(2)设∠ADO=4x,则∠EDO=x,
∵OA=OD,
∴∠OAD=∠ADO=4x,
∵AB⊥CD,
∴∠AED=90°,
∴∠OAD+∠ADE=90°,
即4x+4x+x=90°,
解得:x=10°,
∴∠ADC=50°,
∴∠AOC=100°,
∴扇形OAC(阴影部分)的面积=$\frac{100×π×{5}^{2}}{360}$=$\frac{125π}{18}$.
点评 本题考查了垂径定理、勾股定理、等腰三角形的性质、圆周角定理、扇形面积的计算;熟练掌握垂径定理和勾股定理,由圆周角定理求出∠AOC是解决(2)的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 乘客 | 甲 | 乙 | 丙 | 丁 | 戍 |
| 输入/公里 | 1.5 | 2 | 4 | 6 | 8 |
| 输出/元 | 5 | 5 | 8 | 11 | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
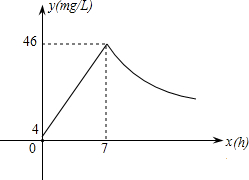 近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题:
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com