
����Ŀ������һ��ʮ�����µ���Ȼ��![]() ������
������![]() ÿ����λ�ϵ��������������
ÿ����λ�ϵ��������������![]() ���������ٰ�ÿһ����������ԭ������λ˳�����У��õ�һ���µ����������������Ϊԭ��
���������ٰ�ÿһ����������ԭ������λ˳�����У��õ�һ���µ����������������Ϊԭ��![]() ����ģ����������Ϊ
����ģ����������Ϊ![]() .��
.��![]() .������ģ�������ļӷ��涨����:������ĩλ���룬�����������ν���Ӧ��λ.�ϵ����ֱ���ӣ��涨:
.������ģ�������ļӷ��涨����:������ĩλ���룬�����������ν���Ӧ��λ.�ϵ����ֱ���ӣ��涨:![]() ��
��![]() ��ӵ�
��ӵ�![]() ;
;![]() ��
��![]() ��ӵ�
��ӵ�![]() ��
��![]() ��ӵ�
��ӵ�![]() ���������һλ��
���������һλ��![]() .��
.��![]() ����ģ������
����ģ������![]() ��ӵ������������ͼ��ʾ.
��ӵ������������ͼ��ʾ.

�������ϲ��ϣ������������:
(1)![]() ��ֵΪ______ ��
��ֵΪ______ ��![]() ��ֵΪ_
��ֵΪ_
(2)���������Ȼ���ĺ͵���ģ�����������ǵ���ģ�������ĺ���ȣ��������������ģ����Ӳ�����.��![]() ����Ϊ
����Ϊ![]() ������
������![]() ����
����![]() ��
��![]() ������ģ����Ӳ�����.
������ģ����Ӳ�����.
���ж�![]() ������������Щ��
������������Щ��![]() ��ģ����Ӳ���������˵�����ɣ�
��ģ����Ӳ���������˵�����ɣ�
����![]() ��ģ����Ӳ���������λ����______��
��ģ����Ӳ���������λ����______��
���𰸡���1��1011��1101����2����12��65��97������������38
��������
(1) ������ģ�������Ķ�����㼴�ɣ�
(2) �ٸ�����ģ��������ģ����Ӳ������Ķ��壬�ֱ����![]() ��12+23��65+23,97+23��ֵ�����ɵó���
��12+23��65+23,97+23��ֵ�����ɵó���
������λ����ʮλ����Ϊa����λ����Ϊb������a��b����ż�Ժ���ģ��������ģ����Ӳ������Ķ���������ۣ��Ӷ��ó���![]() ��ģ����Ӳ���������λ���ĸ���
��ģ����Ӳ���������λ���ĸ���
��: (1) ![]() ��
��![]()
�ʴ�Ϊ��![]()
![]() ��
��![]() ��
��
![]()
![]() ��
��
![]() ��
��![]() ������ģ����Ӳ�����.
������ģ����Ӳ�����.
![]() ����
����
![]()
![]() ��
��
![]() ��
��![]() ��������ģ����Ӳ�����.
��������ģ����Ӳ�����.
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ������ģ����Ӳ�����
������ģ����Ӳ�����
�ڵ�����λ��С��77ʱ������λ����ʮλ����Ϊa����λ����Ϊb��![]() ��
��
��aΪż����bΪż��ʱ![]() ��
��
��![]()
����![]() ������ģ����Ӳ�������12����28��48��68�����ϣ�
������ģ����Ӳ�������12����28��48��68�����ϣ�
��aΪż����bΪ����ʱ![]() ��
��
��![]()
����![]() ��������ģ����Ӳ�����.��27��47��67��29��49��69���Ϲ�6��
��������ģ����Ӳ�����.��27��47��67��29��49��69���Ϲ�6��
��aΪ������bΪ����ʱ![]() ��
��
��![]()
����![]() ��������ģ����Ӳ�����.��17��37��57��19��39��59Ҳ������
��������ģ����Ӳ�����.��17��37��57��19��39��59Ҳ������
��aΪ������bΪż��ʱ![]() ��
��
��![]()
����![]() ������ģ����Ӳ�������16������18��38��58�����ϣ�
������ģ����Ӳ�������16������18��38��58�����ϣ�
������λ�����ڵ���77ʱ�����Ϲ���4��
������������12+6+16+4=38
�ʴ�Ϊ��38



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ҫ��ͼ(��д����,������ͼ�ۼ�)
(1)����AOB=90��;
(2)�ڡ�AOB�⻭��BOC=60��;
(3)�ֱ�AOB,��AOC�Ľ�ƽ����OD,OE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1����![]() ��ֱ��
��ֱ��![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ������
������![]() ƽ��
ƽ��![]() .
.
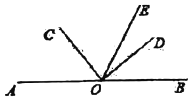
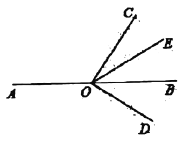
ͼ1 ͼ2
��1����![]() �Ķ�����
�Ķ�����
��2����ͼ1��![]() ��˳ʱ�뷽��ת��ͼ2��ʾ��λ�ã�
��˳ʱ�뷽��ת��ͼ2��ʾ��λ�ã�![]() ��Ȼƽ��
��Ȼƽ��![]() ��
��![]() ����
����![]() ___________.���ú���
___________.���ú���![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����AM��BN�ֱ�����O�����ڵ�A��B��CD��AM��BN�ڵ�D��C��DOƽ����ADC.
��1����֤��CD����O�����ߣ�
��2����AD��4��AB��x (x > 0)��BC��y (y > 0). ��y����x�ĺ�������ʽ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D��E��F�ֱ��ڱ�AB��BC��CA�ϣ���DE��CA��DF��BA��
��������˵�������ı���AEDF��ƽ���ı��Σ��������BAC=90�㣬��ô�ı���AEDF�Ǿ��Σ������ADƽ����BAC����ô�ı���AEDF�����Σ������AD��BC��AB=AC����ô�ı���AEDF�����Σ�
���У���ȷ���У� �� ����

A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ, ��֪������![]() ����A��-2��0����B��4��0����C��0��4�����㣮
����A��-2��0����B��4��0����C��0��4�����㣮
��1����������ߵĽ���ʽ��
��2���������������ֵ������Сֵ���������������Сֵ��
��3������D��2��m���ڴ��������ϣ���y������������Ƿ���ڵ�P��ʹ����BDP�ǵ��������Σ������ڣ���������з���������P������ꣻ�������ڣ���˵�����ɣ�
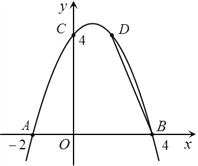
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��4a����A����1��0����C��0��4�����㣬��x�ύ����һ��B��
��1���������ߵĽ���ʽ��
��2���������ߵĶ�������
��3����֪��D��m��m+1���ڵ�һ�����������ϣ����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����ADE�У���BAC=��DAE=90����AB=AC��AD=AE����C��D��E������ͬһ��ֱ���ϣ�����BD��BE�������ĸ����ۣ���BD=CE����BD��CE���ۡ�ACE+��DBC=45�����ܡ�ACE=��DBC���н�����ȷ�ĸ����У� ��

A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��D���߶�AB�ϣ���PCD�ǵȱ������Σ���ACP�ס�PDB��
��1������˵��CD2=ACBD��
��2�����APB�Ķ�����
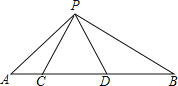
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com