
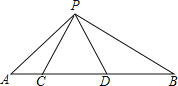
【题目】如图,点C,D在线段AB上,△PCD是等边三角形,△ACP∽△PDB,
(1)请你说明CD2=ACBD;
(2)求∠APB的度数.
【答案】(1)见解析;(2)∠APB=120°.
【解析】
(1)由△ACP∽△PDB,根据相似三角形的对应边成比例,可得AC:PD=PC:BD,又由△PCD是等边三角形,即可证得CD2=ACBD;
(2)由△ACP∽△PDB,根据相似三角形对应角相等,可得∠A=∠BPD,又由△PCD是等边三角形,即可求得∠APB的度数.
(1)证明:∵△ACP∽△PDB,
∴AC:PD=PC:BD,
∴PDPC=ACBD,
∵△PCD是等边三角形,
∴PC=CD=PD,
∴CD2=ACBD;
(2)解:∵△ACP∽△PDB,
∴∠A=∠BPD,
∵△PCD是等边三角形,
∴∠PCD=∠CPD=60°,
∴∠PCD=∠A+∠APC=60°,
∴∠APC+∠BPD=60°,
∴∠APB=∠APC+∠CPD+∠BPD=120°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】给定一个十进制下的自然数![]() ,对于
,对于![]() 每个数位上的数,求出它除以
每个数位上的数,求出它除以![]() 的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数
的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数![]() 的“模二数”,记为
的“模二数”,记为![]() .如
.如![]() .对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位.上的数分别相加,规定:
.对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位.上的数分别相加,规定:![]() 与
与![]() 相加得
相加得![]() ;
;![]() 与
与![]() 相加得
相加得![]() 与
与![]() 相加得
相加得![]() ,并向左边一位进
,并向左边一位进![]() .如
.如![]() 的“模二数”
的“模二数”![]() 相加的运算过程如下图所示.
相加的运算过程如下图所示.

根据以上材料,解决下列问题:
(1)![]() 的值为______ ,
的值为______ ,![]() 的值为_
的值为_
(2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数“模二相加不变”.如![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() 与
与![]() 满足“模二相加不变”.
满足“模二相加不变”.
①判断![]() 这三个数中哪些与
这三个数中哪些与![]() “模二相加不变”,并说明理由;
“模二相加不变”,并说明理由;
②与![]() “模二相加不变”的两位数有______个
“模二相加不变”的两位数有______个
查看答案和解析>>
科目:初中数学 来源: 题型:
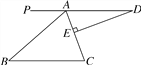
【题目】如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对[Q,R]的好点.
根据下列题意解答问题:
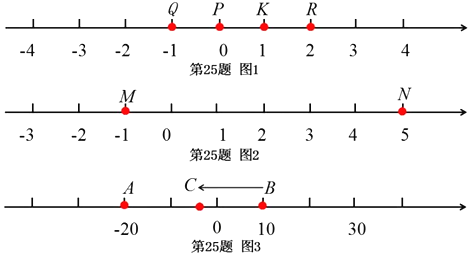
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R
表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是
有序点对![]() 的好点,但点K不是有序点对
的好点,但点K不是有序点对![]() 的好点.同理可以判断:
的好点.同理可以判断:
点P__________有序点对![]() 的好点,点R______________有序点对
的好点,点R______________有序点对![]() 的好点(填“是”或“不是”);
的好点(填“是”或“不是”);
(2)如图2,数轴上点M表示的数为-1,点N表示的数为5,若点X是有序点对![]() 的好点,求点X所表示的数,并说明理由?
的好点,求点X所表示的数,并说明理由?
(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从
点B出发,以每秒2个单位的速度向左运动t秒.当点A、B、C中恰有一个点为其余两有序点对的好点,求t的所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.

(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com