
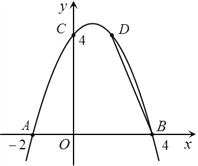
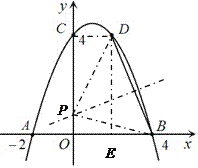
【题目】如图, 已知抛物线![]() 经过A(-2,0)、B(4,0)、C(0,4)三点.
经过A(-2,0)、B(4,0)、C(0,4)三点.
(1)求此抛物线的解析式;
(2)此抛物线有最大值还是最小值?请求出其最大或最小值;
(3)若点D(2,m)在此抛物线上,在y轴的正半轴上是否存在点P,使得△BDP是等腰三角形?若存在,请求出所有符合条件的P点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ;(3)符合条件的
;(3)符合条件的![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
【解析】分析:(1)将A(-2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c,运用待定系数法即可求出此抛物线的解析式;
(2)由于二次项系数a=-![]() <0,所以抛物线有最大值,最大值为
<0,所以抛物线有最大值,最大值为![]() ,代入计算即可;
,代入计算即可;
(3)先将点D(2,m)代入(1)中所求的抛物线的解析式,求出m的值,得到点D的坐标,然后假设在y轴的正半轴上存在点P(0,y)(y>0),使得△BDP是等腰三角形,再分三种情况进行讨论:①PB=PD;②BP=BD;③DP=DB;每一种情况都可以根据两点间的距离公式列出关于y的方程,解方程即可.
详解:(1)将A(-2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c,得
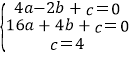 ,
,
解得: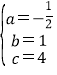 ,
,
所以此抛物线的解析式为y=-![]() x2+x+4;
x2+x+4;
(2)∵y=-![]() x2+x+4,a=-
x2+x+4,a=-![]() <0,
<0,
∴抛物线有最大值,最大值为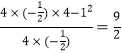 ;
;
(3)∵点D(2,m)在抛物线y=-![]() x2+x+4上,
x2+x+4上,
∴m=-![]() ×22+2+4=4,
×22+2+4=4,
∴D(2,4),
∵B(4,0),
∴BD=![]() .
.
假设在y轴的正半轴上存在点P(0,y)(y>0),使得△BDP是等腰三角形,分三种情况:
①如果PB=PD,那么42+y2=22+(y-4)2,解得y=![]() ,
,
所以P1(0,![]() );
);
②如果BP=BD,那么42+y2=20,解得y=±2(负值舍去),
所以P2(0,2);
③如果DP=DB,那么22+(y-4)2=20,解得y=0或8,
y=0不合题意舍去,
y=8时,(0,8)与D,B三点共线,不合题意舍去;
综上可知,所有符合条件的P点的坐标为P1(0,![]() ),P2(0,2).
),P2(0,2).


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
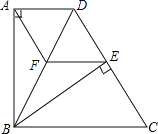
【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按下列方式搭建三角形:
![]()
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | 3 | 5 | 7 | 9 | … |
(1)当三角形的个数为n时,火柴棒的根数是多少?
(2)求当n=100时,有多少根火柴棒?
(3)当火柴棒的根数为2017时,三角形的个数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;
⑤若![]() 的弦AB,CD交于点P,则
的弦AB,CD交于点P,则![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定一个十进制下的自然数![]() ,对于
,对于![]() 每个数位上的数,求出它除以
每个数位上的数,求出它除以![]() 的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数
的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数![]() 的“模二数”,记为
的“模二数”,记为![]() .如
.如![]() .对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位.上的数分别相加,规定:
.对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位.上的数分别相加,规定:![]() 与
与![]() 相加得
相加得![]() ;
;![]() 与
与![]() 相加得
相加得![]() 与
与![]() 相加得
相加得![]() ,并向左边一位进
,并向左边一位进![]() .如
.如![]() 的“模二数”
的“模二数”![]() 相加的运算过程如下图所示.
相加的运算过程如下图所示.

根据以上材料,解决下列问题:
(1)![]() 的值为______ ,
的值为______ ,![]() 的值为_
的值为_
(2)如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数“模二相加不变”.如![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() 与
与![]() 满足“模二相加不变”.
满足“模二相加不变”.
①判断![]() 这三个数中哪些与
这三个数中哪些与![]() “模二相加不变”,并说明理由;
“模二相加不变”,并说明理由;
②与![]() “模二相加不变”的两位数有______个
“模二相加不变”的两位数有______个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:(1)①②![]() ③;(2)①③
③;(2)①③![]() ②;(3)②③
②;(3)②③![]() ①.
①.

(1)以上三个命题是真命题的为(直接答题号) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
如图1,线段![]() ,点
,点![]() 在线段
在线段![]() 上,当点
上,当点![]() 是线段
是线段![]() 和线段
和线段![]() 的中点时,线段
的中点时,线段![]() 的长为_________;若点
的长为_________;若点![]() 在线段
在线段![]() 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段![]() 与线段
与线段![]() 之间的数量关系为_________.
之间的数量关系为_________.

(2)应用:
如图3,现有长为40米的拔河比赛专用绳![]() ,其左右两端各有一段(
,其左右两端各有一段(![]() 和
和![]() )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳![]() 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳![]() . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳![]() ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:
①在图中标出点![]() 、点
、点![]() 的位置,并简述画图方法;
的位置,并简述画图方法;
②请说明①题中所标示![]() 点的理由.
点的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:
①CF=AE;②OE=OF;③图中共有四对全等三角形;④四边形ABCD是平行四边形;其中正确结论的是_____________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com