
【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
如图1,线段![]() ,点
,点![]() 在线段
在线段![]() 上,当点
上,当点![]() 是线段
是线段![]() 和线段
和线段![]() 的中点时,线段
的中点时,线段![]() 的长为_________;若点
的长为_________;若点![]() 在线段
在线段![]() 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段![]() 与线段
与线段![]() 之间的数量关系为_________.
之间的数量关系为_________.

(2)应用:
如图3,现有长为40米的拔河比赛专用绳![]() ,其左右两端各有一段(
,其左右两端各有一段(![]() 和
和![]() )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳![]() 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳![]() . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳![]() ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:
①在图中标出点![]() 、点
、点![]() 的位置,并简述画图方法;
的位置,并简述画图方法;
②请说明①题中所标示![]() 点的理由.
点的理由.

【答案】(1)6;补图见解析,![]() (2)①见解析(答案不唯一)②见解析.
(2)①见解析(答案不唯一)②见解析.
【解析】
(1)如图1,根据线段中点的定义表示出EC和FC的长,则EF=EC+FC=![]() AB,得解;如图2,由EF=EC-FC=
AB,得解;如图2,由EF=EC-FC=![]() AB,得解;
AB,得解;
(2)①如图3,在CD上取一点M,使CM=CA,F为BM的中点,点E与点C重合;
②只要证明CF=20,点F在线段CD上即可.
解:(1)点![]() 在线段
在线段![]() 上时,
上时,
因为点E是线段AC的中点,所以CE=![]() AC,
AC,
因为点F是线段BC的中点,所以CF=![]() BC,
BC,
所以EF=CE+CF=![]() AC+
AC+![]() BC=
BC=![]() AB,
AB,
又AB=12,所以EF=6.
当点![]() 在线段
在线段![]() 的延长线上时,如图2,
的延长线上时,如图2,
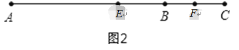
此时,EF=EC-FC═![]() AC-
AC-![]() BC=
BC=![]() AB.
AB.
答案为:6;EF=![]() AB.
AB.
(2)①![]()
图3
如图,在![]() 上取一点
上取一点![]() ,使
,使![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 与点
与点![]() 重合. (答案不唯一)
重合. (答案不唯一)
②因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,
,
所以![]() .
.
因为![]() 米,所以
米,所以![]() 米.
米.
因为![]() 米,
米,![]() 米,
米,
所以![]() 米.
米.
因为点![]() 与点
与点![]() 重合,
重合,![]() 米,
米,
所以![]() 米,所以点
米,所以点![]() 落在线段
落在线段![]() 上.
上.
所以![]() 满足条件.
满足条件.


科目:初中数学 来源: 题型:
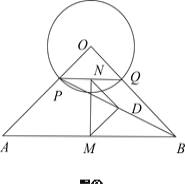
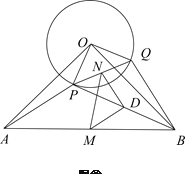
【题目】如图本题图①,在等腰Rt![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,以
上一点,以![]() 为半径作
为半径作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,线段
,线段![]() 、
、![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() 、
、![]() .
.
(1)试探究![]() 是什么特殊三角形?说明理由;
是什么特殊三角形?说明理由;
(2)将![]() 绕点
绕点![]() 逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
(3)若![]() ,把
,把![]() 绕点
绕点![]() 在平面内自由旋转,求
在平面内自由旋转,求![]() 的面积y的最大值与最小值的差.
的面积y的最大值与最小值的差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
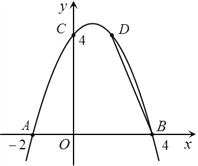
【题目】如图, 已知抛物线![]() 经过A(-2,0)、B(4,0)、C(0,4)三点.
经过A(-2,0)、B(4,0)、C(0,4)三点.
(1)求此抛物线的解析式;
(2)此抛物线有最大值还是最小值?请求出其最大或最小值;
(3)若点D(2,m)在此抛物线上,在y轴的正半轴上是否存在点P,使得△BDP是等腰三角形?若存在,请求出所有符合条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标
(3)已知点D(m,m+1)在第一象限的抛物线上,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过![]() km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方![]() m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为![]() m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连结BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC其中结论正确的个数有( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
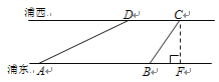
【题目】如图,世博园段的浦江两岸互相平行,C、D是浦西江边间隔200m的两个场馆.海宝在浦东江边的宝钢大舞台A处,测得∠DAB=30°, 然后沿江边走了500m到达世博文化中心B处,测得∠CBF=60°, 求世博园段黄浦江的宽度(结果可保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com