【题目】已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P．
（1）求证：AP=BQ；
（2）在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于PQ的长．
【答案】（1）证明见解析；（2）①AQ﹣AP=PQ，②AQ﹣BQ=PQ，③DP﹣AP=PQ，④DP﹣BQ=PQ.
【解析】试题分析：（1）利用AAS证明△AQB≌△DPA，可得AP=BQ；（2）根据AQ﹣AP=PQ和全等三角形的对应边相等可写出4对线段.
试题解析：（1）在正方形中ABCD中，AD=BA，∠BAD=90°，∴∠BAQ+∠DAP=90°，∵DP⊥AQ，∴∠ADP+∠DAP=90°，∴∠BAQ=∠ADP，∵AQ⊥BE于点Q，DP⊥AQ于点P，∴∠AQB=∠DPA=90°，∴△AQB≌△DPA（AAS），
∴AP=BQ.（2）①AQ﹣AP=PQ，②AQ﹣BQ=PQ，③DP﹣AP=PQ，④DP﹣BQ=PQ.
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】七（1）班的学习小组学习“线段中点”内容时，得到一个很有意思的结论，请跟随他们一起思考.
（1）发现：
如图1，线段
，点
在线段
上，当点
是线段
和线段
的中点时，线段
的长为_________；若点
在线段的延长线上，其他条件不变（请在图2中按题目要求将图补充完整），得到的线段与线段之间的数量关系为_________.
（2）应用：
如图3，现有长为40米的拔河比赛专用绳，其左右两端各有一段（和
）磨损了，磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳和一把剪刀（剪刀只用于剪断麻绳）就可以得到一条长20米的拔河比赛专用绳. 小明所在学习小组认为此法可行，于是他们应用“线段中点”的结论很快做出了符合要求的专用绳，请你尝试着“复原”他们的做法：
①在图中标出点
、点
的位置，并简述画图方法；
②请说明①题中所标示点的理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：已知Q、K、R为数轴上三点，若点K到点Q的距离是点K到点R的距离的2倍，我们就称点K是有序点对[Q，R]的好点．
根据下列题意解答问题：
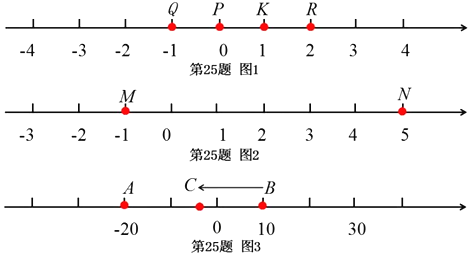
（1）如图1，数轴上点Q表示的数为1，点P表示的数为0，点K表示的数为1，点R
表示的数为2．因为点K到点Q的距离是2，点K到点R的距离是1，所以点K是
有序点对
的好点，但点K不是有序点对
的好点．同理可以判断：
点P__________有序点对的好点，点R______________有序点对
的好点（填“是”或“不是”）；
（2）如图2，数轴上点M表示的数为-1，点N表示的数为5，若点X是有序点对
的好点，求点X所表示的数，并说明理由？
（3）如图3，数轴上点A表示的数为20，点B表示的数为10．现有一只电子蚂蚁C从
点B出发，以每秒2个单位的速度向左运动t秒．当点A、B、C中恰有一个点为其余两有序点对的好点，求t的所有可能的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）
A. 当AB=BC时，四边形ABCD是菱形
B. 当AC⊥BD时，四边形ABCD是菱形
C. 当∠ABC=90°时，四边形ABCD是矩形
D. 当AC=BD时，四边形ABCD是正方形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．
（1）判断BE与CF的数量关系，并说明理由；
（2）如果AB=8，AC=6，求AE、BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，已知⊙O的半径为1，PQ是⊙O的直径，n个相同的正三角形沿PQ排成一列，所有正三角形都关于PQ对称，其中第一个△A1B1C1的顶点A1与点P重合，第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn，Cn在圆上.
(1)如图②，当n＝1时，求正三角形的边长a1.
(2)如图③，当n＝2时，求正三角形的边长a2.
(3)如图①，求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1) 知识储备
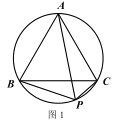
①如图 1，已知点 P 为等边△ABC 外接圆的弧BC 上任意一点．求证：PB+PC= PA.
②定义：在△ABC 所在平面上存在一点 P，使它到三角形三顶点的距离之和最小，则称点 P 为△ABC
的费马点，此时 PA+PB+PC 的值为△ABC 的费马距离．
(2)知识迁移
①我们有如下探寻△ABC (其中∠A，∠B，∠C 均小于 120°)的费马点和费马距离的方法：
如图 2，在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆，根据(1)的结论，易知线段____的长度即为△ABC 的费马距离.
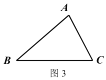
②在图 3 中，用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题（正确的打√，错误的打×）：
ⅰ.任意三角形的费马点有且只有一个（__________）；
ⅱ.任意三角形的费马点一定在三角形的内部（__________）.
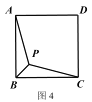
②已知正方形 ABCD，P 是正方形内部一点，且 PA+PB+PC 的最小值为
，求正方形 ABCD 的
边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在矩形ABCD中，M，N分别是边AD、BC的中点，E，F分别是线段BM，CM的中点．
（1）求证：BM＝CM；
（2）判断四边形MENF是什么特殊四边形，并证明你的结论；
（3）当矩形ABCD的长和宽满足什么条件时，四边形MENF是正方形？为什么？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
