
如图:长方形纸片ABCD放置在平面直角坐标系中,A与原点O 重合.B、D分别在x轴和y轴上,AB=8,AD=6.
(1)直接写出C点坐标;
(2)如图①折叠△CEB使B落在线段AC的B处,折痕为CE,求E点坐标;
(3)如图②点P在线段DC上,若△PAB为等腰三角形,试求满足条件的所有P点坐标.


【考点】四边形综合题.
【分析】(1)根据四边形ABCD是矩形,于是得到CD=AB=8,BC=AD=6,∠ADC=∠CBA=90°,即可求得C(8,6);
(2)在Rt△ABC中,根据勾股定理得到AC= =10,根据折叠的性质得到CB1=6,B1E=BE,∠CB1E=∠EBC=90°,于是得到AB1=4,∠AB1E=90°,根据勾股定理列方程即可得到结论;
=10,根据折叠的性质得到CB1=6,B1E=BE,∠CB1E=∠EBC=90°,于是得到AB1=4,∠AB1E=90°,根据勾股定理列方程即可得到结论;
(3)如图②,若△PAB为等腰三角形:①当PA=PB,即点P在AB的垂直平分线上,于是得到P(4,6);②当AB=AP=8,根据勾股定理得到DP=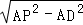 =
=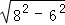 =2
=2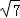 ,求得P(2
,求得P(2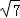 ,6);③当BA=BP=8,根据勾股定理得到即CP2+62=82求得P(8﹣2
,6);③当BA=BP=8,根据勾股定理得到即CP2+62=82求得P(8﹣2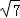 ,0).
,0).
【解答】解:(1)∵四边形ABCD是矩形,
∴CD=AB=8,BC=AD=6,∠AD C=∠CBA=90°,
C=∠CBA=90°,
∴C(8,6);
(2)在Rt△ABC中,AC= =10,
=10,
∵折叠△CEB使B落在线段AC的B处,
∴△BCE≌△B1CE,
∴CB1=6,B1E=BE,∠CB1E=∠EBC=90°,
∴AB1=4,∠AB1E=90°,
∴AE2=AB12+B1E2,
即AE2=42+(8﹣AE)2,
解得:AE=5,∴E(5,0);
(3)如图②,若△PAB为等腰三角形,
①当PA=PB,即点P在AB的垂直平分线上,
∴P(4,6);
②当AB=AP=8,
∴DP=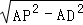 =
=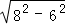 =2
=2 ,
,
∴P(2 ,6);
,6);
③当BA=BP=8,CP2+BC2=BP2,即CP2+62=82,
∴PC=2 ,
,
∴DP=8﹣2 ,
,
∴P(8﹣2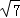 ,0);
,0);
综上所述:若△PAB为等腰三角形,P点坐标为:(8﹣2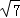 ,0),(4,0)(2
,0),(4,0)(2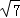 ,0).
,0).



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
从1月15日起,小明连续8天每天晚上记录了家中天然气表显示的读数(如下表):
| 日期 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 | 21日 | 22日 |
| 天然气表读数(单位:m3) | 220 | 229 | 241 | 249 | 259 | 270 | 279 | 290 |
小明的父亲买了一张面值600元的天然气使用卡,已知天然气每立方米1.70元,请估计这张卡是否够小明家用一个月(按30天计算),将结果填在后面的横线上.(只填“够”或“不够”)结果为:______.并说明为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
细心观察图形,认真分析各式,然后解答问题。(10分)




…… ……
(1)请用含有n(n是正整数)的等式表示上述变化规律.
(2)推算出 的长.
的长.
(3)求出 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知 中,
中, ,
, ,直角
,直角 的顶点
的顶点 是
是 中点,两边
中点,两边 ,
, 分别交
分别交 ,
, 于点
于点 ,
, ,给出以下五个结论:
,给出以下五个结论:
①△PFA≌△PEB,②EF=AP,③ ,④
,④ ,⑤
,⑤ ,当
,当 在
在 内绕顶点
内绕顶点 旋转时(点
旋转时(点 不与
不与 ,
, 重合),上述结论中始终正确有( )
重合),上述结论中始终正确有( )
A.2个 B.3个 C.4个 D.5个

查看答案和解析>>
科目:初中数学 来源: 题型:
下列各式从左到右的变形中,是因式分解的是( )
A 3x+2x-1=5x-1 B (3a+2b)(3a—2b)=9a2-4b2
C x2+x=x2(1+ ) D 2x2—8y2=2(x+2y)(x-2y)
) D 2x2—8y2=2(x+2y)(x-2y)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com