
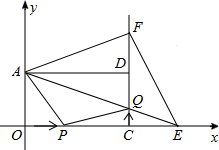
 如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2$\sqrt{5}$.
如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2$\sqrt{5}$.分析 (1)利用勾股定理求出PC的长度,然后利用矩形的性质确定D点的坐标;自变量的取值范围由动点到达终点的时间来确定;
(2)本问关键是利用相似三角形与翻折变换的性质,求出S的表达式.注意求图形面积的方法S=S梯形AOCF+S△FCE-S△AOE.经化简计算后,S=32为定值,所以S不变.
解答 解:(1)由题意可知,当t=2(秒)时,OP=4,CQ=2,
在Rt△PCQ中,由勾股定理得:PC=$\sqrt{{PQ}^{2}{-CQ}^{2}}$$\sqrt{{(2\sqrt{5})}^{2}{-2}^{2}}$=4,
∴OC=OP+PC=4+4=8,
又∵矩形AOCD中,A(0,4),
∴D(8,4).
点P到达终点所需时间为$\frac{8}{2}$=4秒,点Q到达终点所需时间为$\frac{4}{1}$=4秒,由题意可知,t的取值范围为:0<t<4.
(2)结论:△AEF的面积S不变化.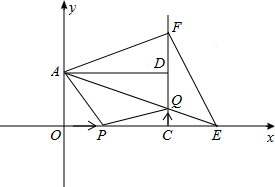
∵AOCD是矩形,
∴AD∥OE,
∴△AQD∽△EQC,
∴$\frac{CE}{AD}$=$\frac{CQ}{DQ}$,∴$\frac{CE}{8}$=$\frac{t}{4-t}$,
∴CE=$\frac{8t}{4-t}$,
由翻折变换的性质可知:DF=DQ=4-t,则CF=CD+DF=8-t.
S=S梯形AOCF+S△FCE-S△AOE
=$\frac{1}{2}$(OA+CF)•OC+$\frac{1}{2}$CF•CE-$\frac{1}{2}$OA•OE
=$\frac{1}{2}$[4+(8-t)]×8+$\frac{1}{2}$(8-t)•$\frac{8t}{4-t}$-$\frac{1}{2}$×4×(8+$\frac{8t}{4-t}$)
化简得:S=32为定值.
∴△AEF的面积S不变化,S=32.
点评 本题考查了坐标平面内平面图形的性质,所涉及的考点包括相似三角形、勾股定理、矩形、翻折变换、动点变化、解方程和分式运算等,翻折变换的性质是解题的关键.


科目:初中数学 来源: 题型:选择题
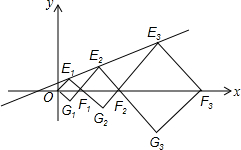 在平面直角坐标系中,点E1,E2,E3,…,和F1,F2,F3,…分别在直线y=kx+b和x轴上,四边形OE1F1G1,四边形F1E2F2G2,四边形F2E3F3G3,…都是正方形,如果E1(1,1),E2(4,2),那么线段Fn-1Fn的长是( )
在平面直角坐标系中,点E1,E2,E3,…,和F1,F2,F3,…分别在直线y=kx+b和x轴上,四边形OE1F1G1,四边形F1E2F2G2,四边形F2E3F3G3,…都是正方形,如果E1(1,1),E2(4,2),那么线段Fn-1Fn的长是( )| A. | 2n-1 | B. | 2n | C. | 22n | D. | 2n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
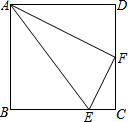 如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,
如图,E、F分别是正方形ABCD中BC和CD边上的点,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF、AE、EF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com