
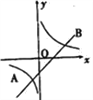
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A、B两点,当y1>y2时,-1<x<0或x>3,则一次函数的解析式为_____________________.
的图象相交于A、B两点,当y1>y2时,-1<x<0或x>3,则一次函数的解析式为_____________________.
科目:初中数学 来源: 题型:
【题目】甲、乙两家批发商出售同样品牌的茶壶和茶杯,定价相同,茶壶每把30元,茶杯每只5元.两家都在进行优惠销售:甲店买一送一大酬宾(买一把茶壶赠送茶杯一只);乙店全场9折优惠(按实际价格的90%收费).某茶具店需茶壶5把,茶杯若干只(不少于5只).
(1)若设购买茶杯x只(x>5),则在甲店购买需付_____元,在乙店购买需付_____元;(用含x的代数式表示)
(2)当茶具店需购买10只茶杯时,到哪家商店购买较便宜?试加以说明;
(3)试求出当茶具店购买多少只茶杯时,在两家商店购买所需付的款一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?(用含a的代数式表示)并说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABN中,∠B =90°,点M是AB上的动点(不与A,B两点重合),点C是BN延长线上的动点(不与点N重合),且AM=BC,CN=BM,连接CM与AN交于点P.
(1)在图1中依题意补全图形;


(2)小伟通过观察、实验,提出猜想:在点M,N运动的过程中,始终有∠APM=45°.小伟把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的一种思路:
要想解决这个问题,首先应想办法移动部分等线段构造全等三角形,证明线段相等,再构造平行四边形,证明线段相等,进而证明等腰直角三角形,出现45°的角,再通过平行四边形对边平行的性质,证明∠APM=45°.
他们的一种作法是:过点M在AB下方作MD![]() AB于点M,并且使MD=CN.通过证明△AMD
AB于点M,并且使MD=CN.通过证明△AMD![]() △CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
△CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
请你参考上面同学的思路,用另一种方法证明∠APM=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD相交于点O,CE//BD,DE//AC.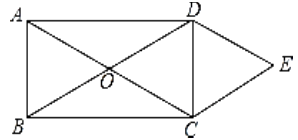
(1)求证:四边形OCED是菱形;
(2)当CD=6,DE=5,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做筝形.如图1,四边形ABCD是一个筝形,其中AD=CD,AB=CB,我们称这个四边形是“筝形ABCD”.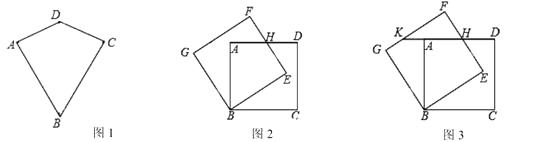
(1)根据筝形的定义判断下列命题是否正确,真命题打“√”,假命题打“×”.
①筝形有一组对角相等.
②菱形是筝形.
③筝形的面积为两条对角线长度的乘积.
(2)如图2,有一个公共顶点B的两个正方形ABCD与正方形BEFG全等,边AD与EF相交于点H.请你判断四边形BEHA是否是“筝形”,说明你的理由;
(3)如图3,当∠EBC=30°时,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,求线段AK的长.
,求线段AK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.
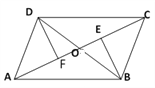
(1)求证:△BOE≌△DOF;
(2)若![]() ,则四边形ABCD是什么特殊四边形?请说明理由.
,则四边形ABCD是什么特殊四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com