
【题目】在△ABN中,∠B =90°,点M是AB上的动点(不与A,B两点重合),点C是BN延长线上的动点(不与点N重合),且AM=BC,CN=BM,连接CM与AN交于点P.
(1)在图1中依题意补全图形;


(2)小伟通过观察、实验,提出猜想:在点M,N运动的过程中,始终有∠APM=45°.小伟把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的一种思路:
要想解决这个问题,首先应想办法移动部分等线段构造全等三角形,证明线段相等,再构造平行四边形,证明线段相等,进而证明等腰直角三角形,出现45°的角,再通过平行四边形对边平行的性质,证明∠APM=45°.
他们的一种作法是:过点M在AB下方作MD![]() AB于点M,并且使MD=CN.通过证明△AMD
AB于点M,并且使MD=CN.通过证明△AMD![]() △CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
△CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
请你参考上面同学的思路,用另一种方法证明∠APM=45°.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
(1)写出第一次移动后这个点在数轴上表示的数为 ;
(2)写出第二次移动后这个点在数轴上表示的数为 ;
(3)写出第五次移动后这个点在数轴上表示的数为 ;
(4)写出第![]() 次移动结果这个点在数轴上表示的数为 ;
次移动结果这个点在数轴上表示的数为 ;
(5)如果第![]() 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导市民绿色出行,提高市民环保意识和健康意识,怀柔区建立了城市公共自行车系统,共建64个站点,投放2300辆自行车.并于2016年8月15日正式投入运营.办理借车卡和借车服务费标准如下:
首次办理借车卡免收工本费,本地居民收取300元保证金及预充值消费50元、外地居民收取500元保证金及预充值消费50元.
借车服务费用实行分段合计,还车刷卡时,从借车卡中结算扣取,每次借车1小时(含)为免费租用期;超过免费租用期1小时以内(含)的收取1元;超过免费租用期2小时到4小时以内(含)的,每小时收取2元;超过免费租用期4个小时以上的,每小时收取3元;一天20元封顶(不足一小时按1小时计).
刘亮妈妈到网点首次办了一张借车卡.第一次,她用了5小时20分钟后才还车.后来妈妈又借车出行了30次,卡中预充值的费用就全部用完了,妈妈说后来的这30次,每次从卡中扣除的服务费都是1元或3元.请你通过列方程或方程组的方法帮刘亮妈妈算一算她扣除1元和3元服务费各几次.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题的是( )
A.两个等边三角形一定相似;
B.两个全等三角形一定相似;
C.有一个锐角相等的两个直角三角形一定相似;
D.有一个锐角相等的两个等腰三角形一定相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,…. 若![]() 和
和![]() 的面积分别为1、9,则
的面积分别为1、9,则![]() 的面积是_________.
的面积是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
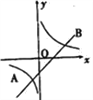
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A、B两点,当y1>y2时,-1<x<0或x>3,则一次函数的解析式为_____________________.
的图象相交于A、B两点,当y1>y2时,-1<x<0或x>3,则一次函数的解析式为_____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com