
【题目】提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,
△PBC与△ABC和△DBC的面积之间有什么关系?
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
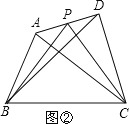
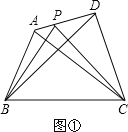
(1)当AP=![]() AD时(如图②):
AD时(如图②):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD.
S△ABD.
∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA.
S△CDA.
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP
=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA
S△CDA
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)
(S四边形ABCD﹣S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(2)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(3)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(4)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
问题解决:当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
【答案】答案见解析
【解析】试题分析:(2)仿照(1)的方法,只需把![]() 换为
换为![]() 即可;
即可;
(3)注意由(1)(2)得到一定的规律;
(4)综合(1)(2)(3)得到面积和线段比值之间的一般关系;
(5)利用(4),得到更普遍的规律.
试题解析:(2)∵![]() △ABP和△ABD的高相等,
△ABP和△ABD的高相等,
![]() 又
又![]() △CDP和△CDA的高相等,
△CDP和△CDA的高相等,
![]()
∴S△PBC=S四边形ABCDS△ABPS△CDP=S四边形ABCD![]() S△ABD
S△ABD![]() S△CDA,
S△CDA,
=S四边形ABCD![]() (S四边形ABCDS△DBC)
(S四边形ABCDS△DBC) ![]() (S四边形ABCDS△ABC),
(S四边形ABCDS△ABC),
![]()
![]()
(3) ![]()
(4) ![]()
![]() △ABP和△ABD的高相等,
△ABP和△ABD的高相等,
![]()
又![]() △CDP和△CDA的高相等,
△CDP和△CDA的高相等,
![]()
∴S△PBC=S四边形ABCDS△ABPS△CDP=S四边形ABCD![]() S△ABD
S△ABD![]() S△CDA,
S△CDA,
=S四边形ABCD![]() (S四边形ABCDS△DBC)
(S四边形ABCDS△DBC) ![]() (S四边形ABCDS△ABC),
(S四边形ABCDS△ABC),
![]()
![]()
问题解决: ![]()


科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与双曲线y=![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释![]() ,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.
,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.

(1)图B可以解释的代数恒等式是 ;
(2)现有足够多的正方形和矩形卡片(如图C),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形(每两块纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使该矩形的面积为![]() ,并利用你所画的图形面积对
,并利用你所画的图形面积对![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(2x,3x-1)是平面直角坐标系上的点。
(1)若点P在第一象限的角平分线上,求x的值;
(2)若点P在第三象限,且到两坐标轴的距离之和为16,求x的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+4交y轴于点A,交抛物线![]() 于点B(3,﹣2),抛物线经过点C(﹣1,0),交y轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.
于点B(3,﹣2),抛物线经过点C(﹣1,0),交y轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.
(1)求抛物线的解析式;
(2)当△PDE为等腰直角三角形时,求出PE的长及P点坐标;
(3)在(2)的条件下,连接PB,将△PBE沿直线AB翻折,直接写出翻折点后E的对称点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
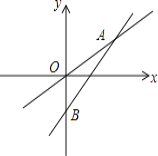
【题目】如图所示是一个正比例函数与一个一次函数的图象,它们交于点A (4,3),一次函数的图象与y轴交于点B,且OA=OB.
(1)求这两个函数的解析式;
(2)当x取何值时,一次函数的值大于正比例函数的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com