
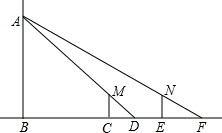
 如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( )
如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( )| A. | 4.5米 | B. | 6米 | C. | 7.2米 | D. | 8米 |
分析 由MC∥AB可判断△DCM∽△DAB,根据相似三角形的性质得$\frac{1.5}{AB}$=$\frac{1}{BC+1}$,同理可得$\frac{1.5}{AB}$=$\frac{2}{BC+3+2}$,然后解关于AB和BC的方程组即可得到AB的长.
解答 解:∵MC∥AB,
∴△DCM∽△DAB,
∴$\frac{DC}{DB}$=$\frac{MC}{AB}$,即$\frac{1.5}{AB}$=$\frac{1}{BC+1}$①,
∵NE∥AB,
∴△FNE∽△FAB,
∴$\frac{NE}{AB}$=$\frac{EF}{BF}$,即$\frac{1.5}{AB}$=$\frac{2}{BC+3+2}$②,
∴$\frac{1}{BC+1}$=$\frac{2}{BC+3+2}$,解得BC=3,
∴$\frac{1.5}{AB}$=$\frac{1}{3+1}$,解得AB=6,
即路灯A的高度AB为6m.
故选B.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


科目:初中数学 来源: 题型:解答题
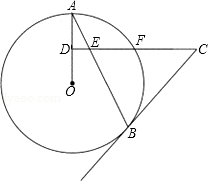 如图,AB是⊙O的弦,点D为OA上的一点,过点D作CD⊥OA于点D,交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,点D为OA上的一点,过点D作CD⊥OA于点D,交弦AB于点E,交⊙O于点F,且CE=CB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -|-5|>0 | B. | -$\frac{4}{7}$>-$\frac{5}{7}$ | C. | |-0.4|<|+0.4| | D. | |-$\frac{1}{2}$|<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
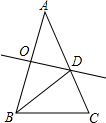 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于O,交AC于D,连接BD.下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④BC=BD,其中正确的结论有①②④.(只需填序号)
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于O,交AC于D,连接BD.下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④BC=BD,其中正确的结论有①②④.(只需填序号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3场 | B. | 4场 | C. | 5场 | D. | 6场 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com