
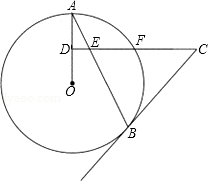
 如图,AB是⊙O的弦,点D为OA上的一点,过点D作CD⊥OA于点D,交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,点D为OA上的一点,过点D作CD⊥OA于点D,交弦AB于点E,交⊙O于点F,且CE=CB.分析 (1)连接OB,由圆的半径相等和已知条件证明∠OBC=90°,即可证明BC是⊙O的切线;
(2)在直角三角形ADE中,由正切函数求得DE,进而求得CE,然后根据勾股定理求得AE,作CG⊥AB于G,由∠AED=∠CEG,得出tan∠CEG=$\frac{4}{3}$,在直角三角形CGE中,由正切函数求得GE,进而求得BE,从而求得AB的长.
解答 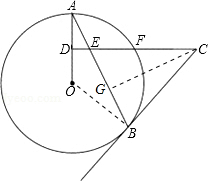 (1)证明:连接OB,
(1)证明:连接OB,
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC,
又∵CD⊥OA,
∴∠A+∠AED=∠A+∠CEB=90°,
∴∠OBA+∠ABC=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:∵AD=4,tan∠AED=$\frac{4}{3}$,
∴tan∠AED=$\frac{AD}{DE}$=$\frac{4}{DE}$=$\frac{4}{3}$,
∴DE=3,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
∵CD=13,
∴CE=CD-DE=13-3=10,
作CG⊥AB于G,
∵∠AED=∠CEG,
∴tan∠CEG=$\frac{4}{3}$,
∴$\frac{CG}{EG}$=$\frac{4}{3}$,
设CG=4a,EG=3a,
在Rt△EGC中,EG2+CG2=CE2,
即(3a)2+(4a)2=102,
解得a=2,
∴EG=3a=6,
∵CE=CB,CG⊥BE,
∴BE=2EG=2×6=12,
∴AB=AE+BE=5+12=17.
点评 此题考查了切线的判定,等腰三角形的性质,锐角三角函数定义,熟练掌握切线的判定方法是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$=$\overrightarrow{BA}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{CA}$ | C. | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | D. | $\overrightarrow{a}$+(-$\overrightarrow{a}$)=$\overrightarrow{0}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
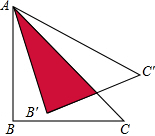 如图,直角△ABC的直角边AB的长为6cm,∠C=30°,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中两三角形重叠部分的面积等18 cm2.
如图,直角△ABC的直角边AB的长为6cm,∠C=30°,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中两三角形重叠部分的面积等18 cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
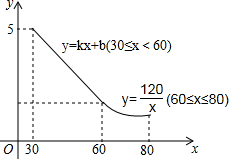 某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格x(元/个)的函数关系如图所示.
某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格x(元/个)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
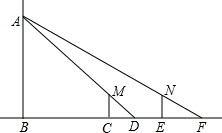 如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( )
如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( )| A. | 4.5米 | B. | 6米 | C. | 7.2米 | D. | 8米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com