

分析 先画出几何图形,如图,CD=EF=BH=1.6m,CE=DF=36m,∠ADH=30°,∠AFH=30°,分别利用正切定义得到FH=$\frac{AH}{tan60°}$,DH=$\frac{AH}{tan30°}$,则$\frac{AH}{tan30°}$-$\frac{AH}{tan60°}$=36,再利用特殊角的函数值可计算出AH=18$\sqrt{3}$,然后计算AH+BH即可.
解答 解:如图,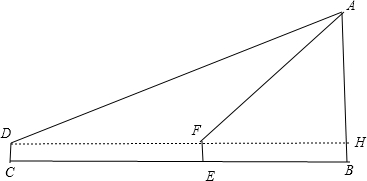 CD=EF=BH=1.6m,CE=DF=36m,∠ADH=30°,∠AFH=30°,
CD=EF=BH=1.6m,CE=DF=36m,∠ADH=30°,∠AFH=30°,
在Rt△AHF中,∵tan∠AFH=$\frac{AH}{FH}$,
∴FH=$\frac{AH}{tan60°}$,
在Rt△ADH中,∵tan∠ADH=$\frac{AH}{DH}$,
∴DH=$\frac{AH}{tan30°}$,
而DH-FH=DF,
∴$\frac{AH}{tan30°}$-$\frac{AH}{tan60°}$=36,即$\frac{AH}{\frac{\sqrt{3}}{3}}$-$\frac{AH}{\sqrt{3}}$=36,
∴AH=18$\sqrt{3}$,
∴AB=AH+BH=18$\sqrt{3}$+1.6≈33(m).
答:纪念塔的高度约为33m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


科目:初中数学 来源: 题型:解答题
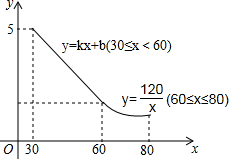 某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格x(元/个)的函数关系如图所示.
某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格x(元/个)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
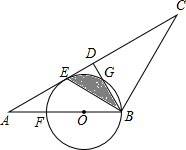 已知,如图,在△ABC中,AB=BC,D是AC的中点,BE平分∠ABD交AC于点E,点O是AB边上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
已知,如图,在△ABC中,AB=BC,D是AC的中点,BE平分∠ABD交AC于点E,点O是AB边上一点,⊙O过B、E两点,交BD于点G,交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
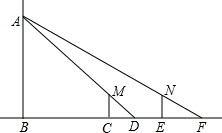 如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( )
如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( )| A. | 4.5米 | B. | 6米 | C. | 7.2米 | D. | 8米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
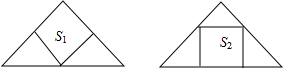 如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )
如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com