【题目】某学校有3名老师决定带领
名小学生去植物园游玩，有两家旅行社可供选择，甲旅行社的收费标准为老师全价，学生七折优惠；而乙旅行社不分老师和学生一律八折优惠，这两家旅行社全价都是每人500元.
（1）用代数式表示这3位老师和名学生分别在甲、乙两家旅行社的总费用；
（2）如果这两家旅行社的总费用一样，那么老师可以带几名学生？
导学与测试系列答案
新非凡教辅冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】江南农场收割小麦，已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷，2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷．
（1）每台大型收割机和每台小型收割机1小时收割小麦各多少公顷？
（2）大型收割机每小时费用为300元，小型收割机每小时费用为200元，两种型号的收割机一共有10台，要求2小时完成8公顷小麦的收割任务，且总费用不超过5400元，有几种方案？请指出费用最低的一种方案，并求出相应的费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A（m，6），B（n，1）在反比例函数y=
的图象上，AD⊥x轴于点D，BC⊥x轴于点C，点E在CD上，CD=5，△ABE的面积为10，则点E的坐标是（ ）
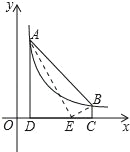
A. （3，0） B. （4，0） C. （5，0） D. （6，0）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】补全解答过程：
（1）如图，线段AC=4，线段BC=9，点M是AC的中点，在CB上取一点N，CN：NB=1:2，求MN的长．
解：∵M是AC的中点，AC=4，
∴MC=
（填线段名称）= ，
又因为CN：NB=1：2，BC=9，
∴CN=
（填线段名称）= ．
∴MN= （填线段名称）+ （填线段名称）=5．
∴MN的长为5．
（2）已知：如图，直线AB∥CD，直线EF与直线AB，CD分别交于点G，H；GM平分∠FGB，∠3＝60°．求∠1的度数．
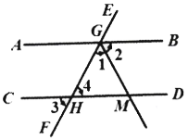
解：∵EF与CD交于点H，（已知）
∴∠3＝∠4．（ ）
∵∠3＝60°，（ ）
∴∠4＝60°．
∵AB∥CD，EF与AB，CD交于点G，H，（已知）
∴∠4+∠FGB＝180°．（ ）
∴∠FGB＝ ．
∵GM平分∠FGB，（已知）
∴∠1＝ °．（角平分线的定义）
查看答案和解析>>
科目：初中数学 来源： 题型：
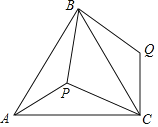
【题目】如图，P是正三角形ABC内的一点，且PA=6，PB=8，PC=10，若将△PAC绕点A逆时针旋转后得到△P′AB．
（1）求点P与点P′之间的距离；
（2）求∠APB的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
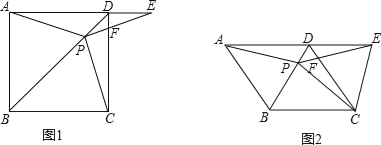
【题目】如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．
（1）证明：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使三角形AMN周长最小时，则∠AMN+∠ANM的度数为（ ）
A. 80° B. 90° C. 100° D. 130°
查看答案和解析>>
科目：初中数学 来源： 题型：
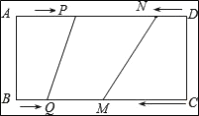
【题目】如图，在矩形ABCD中，BC=24cm，P，Q，M，N分别从A，B，C，D出发沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．
已知在相同时间内，若BQ=x cm（x≠0），则AP=2x cm，CM=3x cm，DN=x2cm．
（1）当x为何值时，以P、N两点重合？
（2）问Q、M两点能重合吗？若Q、M两点能重合，则求出相应的x的值；若Q、M两点不能重合，请说明理由．
（3）当x为何值时，以P，Q，M，N为顶点的四边形是平行四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把几个数用大括号围起来，中间用逗号隔开.如：
，我们称之为集合，其中的数称其为集合的元素.如果一个集合满足：当有理数a是集合的元素时，有理数-4-a也必是这个集合的元素，这样的集合我们称为友好集合.
(1)请你判断集合
，
是不是友好集合？
(2)请你写出满足条件的两个友好集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
