
【题目】补全解答过程:
(1)如图,线段AC=4,线段BC=9,点M是AC的中点,在CB上取一点N,CN:NB=1:2,求MN的长.
![]()
解:∵M是AC的中点,AC=4,
∴MC=![]() (填线段名称)= ,
(填线段名称)= ,
又因为CN:NB=1:2,BC=9,
∴CN=![]() (填线段名称)= .
(填线段名称)= .
∴MN= (填线段名称)+ (填线段名称)=5.
∴MN的长为5.
(2)已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
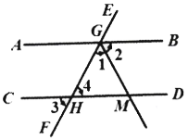
解:∵EF与CD交于点H,(已知)
∴∠3=∠4.( )
∵∠3=60°,( )
∴∠4=60°.
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.( )
∴∠FGB= .
∵GM平分∠FGB,(已知)
∴∠1= °.(角平分线的定义)
【答案】(1)AC;2;BC;3;MC;NC;(2)对顶角相等;已知;两直线平行,同旁内角互补;120°;60.
【解析】
(1) 根据线段中点的性质,可得MC的长,根据线段长度的比,可得CN的长,根据线段的和差,可得答案;
(2) 依据对顶角相等以及平行线的性质,即可得到∠4=60°,∠FGB=120°,再根据角平分线的定义,即可得出∠1=60°.
(1) 解:∵M是AC的中点,AC=4,
∴MC=![]() AC=2,
AC=2,
又因为CN:NB=1:2,BC=9,
∴NC=![]() BC=3.
BC=3.
∴MN=MC+NC=5.
∴MN的长为5.
故答案为:AC;2;BC;3;MC;NC.
(2) 解:∵EF与CD交于点H,(已知)
∴∠3=∠4.(对顶角相等)
∵∠3=60°,(已知)
∴∠4=60°.
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.(两直线平行,同旁内角互补)
∴∠FGB=120°.
∵GM平分∠FGB,(已知)
∴∠1=60°.(角平分线的定义)
故答案为:对顶角相等;已知;两直线平行,同旁内角互补;120°;60.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
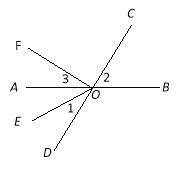
(1)图中∠AOF的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据 可得∠BOD= 度;
(3)如果∠1=32°,求∠2和∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】微信运动和腾讯公益推出了一个爱心公益活动:一天中走路若步数达到10000步及以上,则可通过微信运动和腾讯基金会向公益活动捐款,每步可捐0.0002元;若步数在10000步以下,则不能参与爱心公益捐款.
(1)某天小齐的步数为15000步,求他这天为爱心公益可捐款多少钱?
(2)己知甲、乙、丙三人某天通过步数共捐款8.4元,且甲的步数:乙的步数:丙的步数![]() ,求这天甲走了多少步?
,求这天甲走了多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q 分别在边OB、OA上,则MP+PQ+QN的最小值是_____.
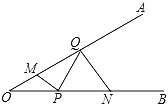
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
编号 类型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(1) 计算甲、乙两种电子钟走时误差的平均数;
(2) 计算甲、乙两种电子钟走时误差的方差;
(3) 根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有3名老师决定带领![]() 名小学生去植物园游玩,有两家旅行社可供选择,甲旅行社的收费标准为老师全价,学生七折优惠;而乙旅行社不分老师和学生一律八折优惠,这两家旅行社全价都是每人500元.
名小学生去植物园游玩,有两家旅行社可供选择,甲旅行社的收费标准为老师全价,学生七折优惠;而乙旅行社不分老师和学生一律八折优惠,这两家旅行社全价都是每人500元.
(1)用代数式表示这3位老师和![]() 名学生分别在甲、乙两家旅行社的总费用;
名学生分别在甲、乙两家旅行社的总费用;
(2)如果这两家旅行社的总费用一样,那么老师可以带几名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公共交通收费如下:
公交票价 | ||
里程(千米) | 票价(元) | 刷卡优惠后付款(元) |
0-10 | 2 | 1 |
10-15 | 3 | 1.5 |
15-20 | 4 | 2 |
20-25 | 5 | 2.5 |
25-30 | 6 | 3 |
以后每增加5千米 | 增加1元 | 增加0.5元 |
地铁票价 | |
里程(千米) | 票价(元) |
0-6 | 3 |
6-12 | 4 |
12-22 | 5 |
22-32 | 6 |
32-52 | 7 |
52-72 | 8 |
以后每增加20千米 | 增加1元 |
(公交票价10千米(含)内2元,不足10千米按10千米计算,其他里程类同;地铁票价6千米(含)内3元,不足6千米按6千米计算,其他里程类同)
(1)张阿姨周日去看望父母,可是张阿姨忘了带一卡通,请你帮助张阿姨思考两个问题:
①若到父母家无论乘公交车还是地铁距离都是24千米,选择哪种公交交通工具费用较少?
②若只用10元钱乘坐公交或地铁,选择哪种公共交通工具乘坐的里程更远?
(2)张阿姨下周日计划使用一卡通刷卡乘公共交通到景点游玩,若里程大于35千米且小于120千米,公交、地铁均可直达.请问:选择公交还是选择地铁出行更省钱?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别沿同一条路线从
,甲、乙两车分别沿同一条路线从![]() 地出发驶往
地出发驶往![]() 地,已知甲车的速度为
地,已知甲车的速度为![]() ,乙车的速度为
,乙车的速度为![]() ,甲车先出发
,甲车先出发![]() 后乙车再出发,乙车到达
后乙车再出发,乙车到达![]() 地后再原地等甲车.
地后再原地等甲车.
(1)求乙车出发多长时间追上甲车?
(2)求乙车出发多长时间与甲车相距![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com