
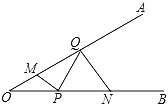
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q 分别在边OB、OA上,则MP+PQ+QN的最小值是_____.
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
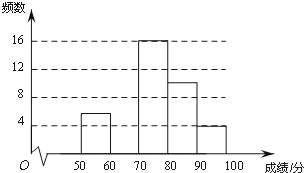
【题目】为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 | a | 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | c | b |
合计 | 50 | 1.00 |
(1)表中的a=______,b=______,c=______;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
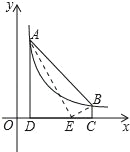
【题目】如图,点A(m,6),B(n,1)在反比例函数y=![]() 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是( )
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是( )
A. (3,0) B. (4,0) C. (5,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在钟面上,点![]() 为钟面的圆心,以点
为钟面的圆心,以点![]() 为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
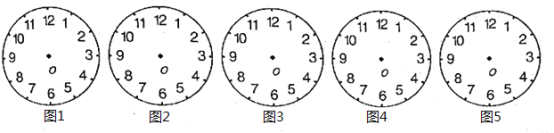
(1)在图1中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图2中画一个直角,使直角的内部含有3个数字,且数字之积等于数字之和;
(3)在图3中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图4中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图5中画两个直角,使这两个直角的内部含有的3个数字之和相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解答过程:
(1)如图,线段AC=4,线段BC=9,点M是AC的中点,在CB上取一点N,CN:NB=1:2,求MN的长.
![]()
解:∵M是AC的中点,AC=4,
∴MC=![]() (填线段名称)= ,
(填线段名称)= ,
又因为CN:NB=1:2,BC=9,
∴CN=![]() (填线段名称)= .
(填线段名称)= .
∴MN= (填线段名称)+ (填线段名称)=5.
∴MN的长为5.
(2)已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
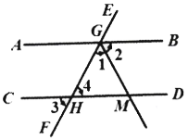
解:∵EF与CD交于点H,(已知)
∴∠3=∠4.( )
∵∠3=60°,( )
∴∠4=60°.
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.( )
∴∠FGB= .
∵GM平分∠FGB,(已知)
∴∠1= °.(角平分线的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
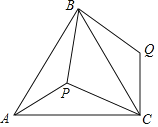
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
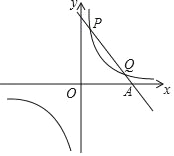
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内P(
的图象交于第一象限内P(![]() ,8),Q(4,m)两点.
,8),Q(4,m)两点.
(1)分别求出这两个函数的表达式;
(2)请直接写出不等式k1x+b<![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com