
【题目】如图,点A(m,6),B(n,1)在反比例函数y=![]() 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是( )
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是( )
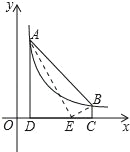
A. (3,0) B. (4,0) C. (5,0) D. (6,0)
【答案】A
【解析】分析:
由题意易得:6m=n,n-m=DC=5,由此即可解得m=1和n=6,设点E的坐标为(x,0),则DE=x-1,CE=6-x,AD=6,BC=1,这样即可由S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE
把S△ABE的面积用含x的代数式表达出来,结合S△ABE=10即可列出关于x的方程,解方程求得x的值即可得到点E的坐标.
详解:
∵点A(m,6),B(n,1)在反比例函数![]() 的图象上,
的图象上,
∴6m=n,n-m=DC=5,
解得:m=1,n=6,
∴点A、B的坐标分别为(1,6)、(6,1),
设点E的坐标为(x,0),则DE=x-1,CE=6-x,
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
连接AE,BE,
则S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE
=![]() (BC+AD)·DC-
(BC+AD)·DC-![]() DE·AD-
DE·AD-![]() CE·BC
CE·BC
=![]()
=![]() .
.
又∵S△ABE=10,
∴![]() ,解得:
,解得:![]() ,
,
∴点E的坐标为(3,0).
故选A.


科目:初中数学 来源: 题型:
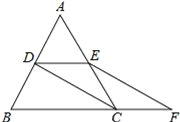
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过E点作EF∥DC交BC的延长线于点F,连接CD.
(1)求证:四边形CDEF是平行四边形;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点C画直线AB的平行线(不写画法,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段_____的长度是点A到直线BC的距离;
(4)线段AG、AH的大小关系为AG_____AH.(填“>”或“<”或“=”),理由________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
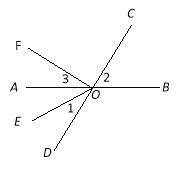
(1)图中∠AOF的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据 可得∠BOD= 度;
(3)如果∠1=32°,求∠2和∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】微信运动和腾讯公益推出了一个爱心公益活动:一天中走路若步数达到10000步及以上,则可通过微信运动和腾讯基金会向公益活动捐款,每步可捐0.0002元;若步数在10000步以下,则不能参与爱心公益捐款.
(1)某天小齐的步数为15000步,求他这天为爱心公益可捐款多少钱?
(2)己知甲、乙、丙三人某天通过步数共捐款8.4元,且甲的步数:乙的步数:丙的步数![]() ,求这天甲走了多少步?
,求这天甲走了多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
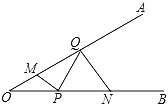
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q 分别在边OB、OA上,则MP+PQ+QN的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有3名老师决定带领![]() 名小学生去植物园游玩,有两家旅行社可供选择,甲旅行社的收费标准为老师全价,学生七折优惠;而乙旅行社不分老师和学生一律八折优惠,这两家旅行社全价都是每人500元.
名小学生去植物园游玩,有两家旅行社可供选择,甲旅行社的收费标准为老师全价,学生七折优惠;而乙旅行社不分老师和学生一律八折优惠,这两家旅行社全价都是每人500元.
(1)用代数式表示这3位老师和![]() 名学生分别在甲、乙两家旅行社的总费用;
名学生分别在甲、乙两家旅行社的总费用;
(2)如果这两家旅行社的总费用一样,那么老师可以带几名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
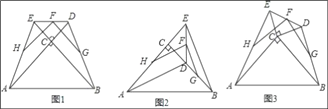
【题目】综合与探究
问题情境:
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com