
【题目】下列各点中,在函数y=﹣2x的图象上的是( )
A.(![]() ,1)B.(﹣
,1)B.(﹣![]() ,1)C.(﹣
,1)C.(﹣![]() ,﹣1) D(0,﹣1)
,﹣1) D(0,﹣1)
【答案】B
【解析】
把四个选项中的点分别代入解析式y=-2x,通过等式左右两边是否相等来判断点是否在函数图象上.
A、把(![]() ,1)代入函数y=-2x得:左边=1,右边=-1,左边≠右边,所以点(
,1)代入函数y=-2x得:左边=1,右边=-1,左边≠右边,所以点(![]() ,1)不在函数y=-2x的图象上,故本选项不符合题意;
,1)不在函数y=-2x的图象上,故本选项不符合题意;
B、把(-![]() ,1)代入函数y=-2x得:左边=1,右边=1,左边=右边,所以点(-
,1)代入函数y=-2x得:左边=1,右边=1,左边=右边,所以点(-![]() ,1)在函数y=-2x的图象上,故本选项符合题意;
,1)在函数y=-2x的图象上,故本选项符合题意;
C、把(-![]() ,-1)代入函数y=-2x得:左边=-1,右边=1,左边≠右边,所以点(-
,-1)代入函数y=-2x得:左边=-1,右边=1,左边≠右边,所以点(-![]() ,-1)不在函数y=-2x的图象上,故本选项不符合题意;
,-1)不在函数y=-2x的图象上,故本选项不符合题意;
D、把(0,-1)代入函数y=-2x得:左边=-1,右边=0,左边≠右边,所以点(0,-1)不在函数y=-2x的图象上,故本选项不符合题意;
故选B.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
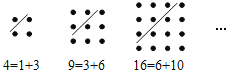
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 | a | 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | c | b |
合计 | 50 | 1.00 |
(1)表中的a=______,b=______,c=______;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
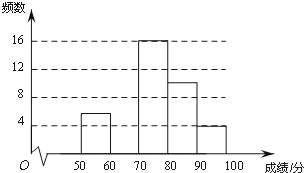
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用双十字相乘法分解因式
例:20x2+9xy-18y2-18x+33y-14。
![]()
∵4×6+5×(-3)=9,4×(-7)+5×2=-13,-3×(-7)+2×6=33,
∴20x2+9xy-18y2-18x+33y-14=(4x-3y+2)(5x+6y-7)。
双十字相乘法的理论根据是多项式的乘法,在使用双十字相乘法时,应注意它带有试验性质,很可能需要经过多次试验才能得到正确答案。
分解因式6x2-5xy-6y2-2xz-23yz-20z2=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数y=![]() 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是( )
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是( )
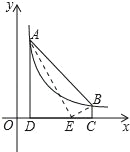
A. (3,0) B. (4,0) C. (5,0) D. (6,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在钟面上,点![]() 为钟面的圆心,以点
为钟面的圆心,以点![]() 为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
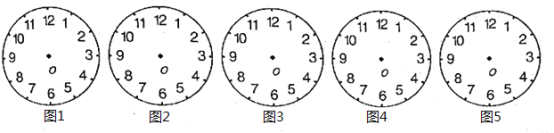
(1)在图1中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图2中画一个直角,使直角的内部含有3个数字,且数字之积等于数字之和;
(3)在图3中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图4中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图5中画两个直角,使这两个直角的内部含有的3个数字之和相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
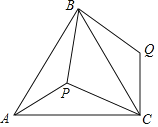
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com