
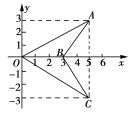
【题目】如图,三角形BCO是三角形BAO经过某种变换得到的.
(1)写出A,C的坐标;
(2)图中A与C的坐标之间的关系是什么?
(3)如果三角形AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?
【答案】(1)A(5,3),C(5,-3)(2)关于x轴对称(3)N(x,-y)
【解析】
(1)根据图形结合坐标系找出点A、C的坐标即可;
(2)根据点A、C横纵坐标的特点,即可得出点A与点C关于x轴对称;
(3)由(2)结合O、B点即可得出△BCO与△BAO关于x轴对称,再由点M的坐标即可得出点N的坐标.
(1)观察图形,可得出点A的坐标为(5,3),点C的坐标为(5,-3).
(2)∵5=5,3+(-3)=0,
∴点A与点C关于x轴对称.
(3)∵点A与点C关于x轴对称,点O、B在x轴上,
∴△BCO与△BAO关于x轴对称,
∵点M(x,y)在△AOB中,
∴与点M对应的点N的坐标为(x,-y).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
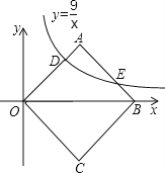
【题目】如图,Rt△AOB中,∠OAB=90°,OA=AB,将Rt△AOB放置于直角坐标系中,OB在x轴上,点O是原点,点A在第一象限.点A与点C关于x轴对称,连结BC,OC.双曲线![]() (x>0)与OA边交于点D、与AB边交于点E.
(x>0)与OA边交于点D、与AB边交于点E.
(1)求点D的坐标;
(2)求证:四边形ABCD是正方形;
(3)连结AC交OB于点H,过点E作EG⊥AC于点G,交OA边于点F,求四边形OHGF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
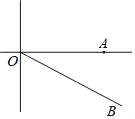
【题目】如图,A城气象台测得台风中心在A城正西方向240km的O处,以每小时30km的速度向南偏东60°的OB方向移动,距台风中心150km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到台风的影响,求出受台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=![]() x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.
(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:等腰三角形两腰上的高相等.

(1)请你写出它的逆命题:______.
(2)逆命题是真命题吗?若是,请证明;若不是,请举出反例(要求:画出图形,写出已知,求证和证明过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:对于一个关于![]() 的一元二次方程
的一元二次方程![]() (其中a≠0,a、b、c为常数)的两根分别为
(其中a≠0,a、b、c为常数)的两根分别为![]() ,
,![]() ,我们有如下发现①若
,我们有如下发现①若![]() ,
,![]() 为整数,则这个一元二次方程的判别式
为整数,则这个一元二次方程的判别式![]() 一定为完全平方数;②
一定为完全平方数;② ![]() ,
,![]() 满足韦达定理:即
满足韦达定理:即![]() ,
,![]() ;
;
③韦达定理也有逆定理,即如果两数![]() 和
和![]() 满足如下关系:
满足如下关系:![]() ,
,![]() ,那么这两个数
,那么这两个数![]() 和
和![]() 是方程
是方程![]() (
(![]() )的两个根.
)的两个根.
请应用上述材料解决以下问题:
(1)若实数![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,
的两个根,
①当![]() 时,则
时,则![]() ,
,![]() ;
;
②若![]() 均为整数且
均为整数且![]() ,求
,求![]() 的值;
的值;
(2)已知实数![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
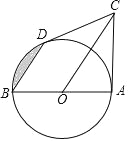
【题目】如图,AB是⊙O的直径,CD切⊙O于点D,且BD∥OC,连接AC.
(1)求证:AC是⊙O的切线;
(2)若AB=OC=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com