练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一根长为5米的竹竿AB斜立于墙MN的右侧，底端B与墙角N 的距离为3米，当竹竿顶端A下滑x米时，底端B便随着向右滑行y米，反映y与x变化关系的大致图象是（ ）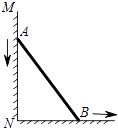

    A.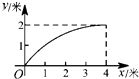
    B.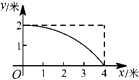
    C.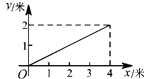
    D.

    【答案】A
    【解析】解：在Rt△ABN中，AB=5米，NB=3米，

    根据勾股定理得：AN= =4米，

    若A下滑x米，AN=（4﹣x）米，

    根据勾股定理得：NB= =3+y，

    整理得：y= ﹣3，

    当x=0时，y=0；当x=4时，y=2，且不是直线变化的，

    故选A．

    【考点精析】解答此题的关键在于理解函数的图象的相关知识，掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米／时，两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示，现有以下4个结论：

    ①快递车从甲地到乙地的速度为100千米／时；②甲、乙两地之间的距离为120千米；③图中点B的坐标为(，75)；④快递车从乙地返回时的速度为90千米／时．以上4个结论中正确的是( )

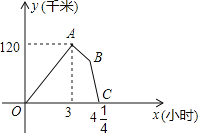
    A. ①③④ B. ①②④ C. ②③④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，ABCD中，E、F分别是边AB、CD的中点．

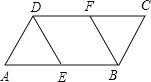
    （1）求证：四边形EBFD是平行四边形；

    （2）若AD=AE=2，∠A=60°，求四边形EBFD的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在四边形ABCD中，∠A=x，∠C=y，（0°＜x＜180°，0°＜y＜180°）．

    （1）∠ABC+∠ADC=_____（用含x、y的代数式表示）；

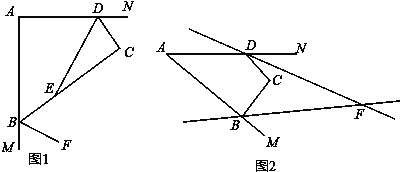
    （2）如图1，若x=y=90°，DE平分∠ADC，BF平分与∠ABC相邻的外角，请写出DE与BF的位置关系，并说明理由．

    （3）如图2，∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角，

    ①当x＜y时，若x+y=140°，∠DFB=30°试求x、y．

    ②小明在作图时，发现∠DFB不一定存在，请直接指出x、y满足什么条件时，∠DFB不存在．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB= ，AC=5，tanA=2，D是BC中点，点P是AC上一个动点，将△BPD沿PD折叠，折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半，则AP的长为 ．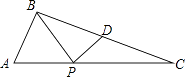

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列长度的三条线段能组成钝角三角形的是( )

    A. 3,4,4 B. 3,4,5 C. 3,4,6 D. 3,4,7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，给出下列条件：①∠1=∠2；②∠3=∠4；③AD∥BC，且∠D=∠B；④AD∥BC，且∠BAD=∠BCD．其中，能推出AB∥DC的条件为（ ）

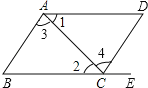
    A．① B．② C．②③ D．②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AE⊥BD，垂足为E，∠DAE：∠BAE=1：2，则∠CAE的度数( )

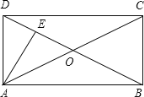
    A. 30° B. 45° C. 60° D. 75°

    查看答案和解析>>

    同步练习册答案