
【题目】已知在四边形ABCD中,∠A=x,∠C=y,(0°<x<180°,0°<y<180°).
(1)∠ABC+∠ADC=_____(用含x、y的代数式表示);
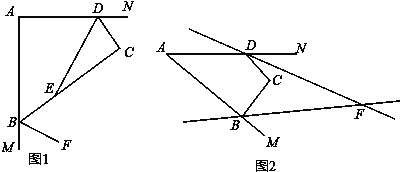
(2)如图1,若x=y=90°,DE平分∠ADC,BF平分与∠ABC相邻的外角,请写出DE与BF的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x<y时,若x+y=140°,∠DFB=30°试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,∠DFB不存在.
【答案】(1)360°-x-y;(2)DE⊥BF,理由见解析;(3)①![]() ;②当x、y满足x=y时,∠DFB不存在.
;②当x、y满足x=y时,∠DFB不存在.
【解析】
(1)利用四边形内角和定理得出答案即可;(2)利用角平分线的性质结合三角形外角的性质得出即可;(3)①利用角平分线的性质以及三角形内角和定理,得出∠DFB=![]() y-
y-![]() x=30°,进而得出x,y的值;②当x=y时,∠ABC、∠ADC相邻的外角平分线所在直线互相平行,此时∠DFB不存在.
x=30°,进而得出x,y的值;②当x=y时,∠ABC、∠ADC相邻的外角平分线所在直线互相平行,此时∠DFB不存在.
(1)∵四边形内角和为(4-2)×180°=360°,
∴∠ABC+∠ADC=360°-x-y,
故答案为:360°-x-y
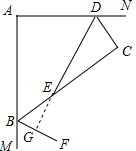
(2)DE⊥BF,理由如下:
如图:延长DE交BF于G,
∵DE平分∠ADC,BF平分∠MBC,
∴∠CDE=![]() ∠ADC,∠CBF=
∠ADC,∠CBF=![]() ∠CBM,
∠CBM,
∵x=y=90°,
∴∠CBM=180°-∠ABC=180°-(180°-∠ADC)=∠ADC,
∴∠CDE=∠CBF,
∵∠BED=∠CDE+∠C=∠CBF+∠BGE,
∴∠BGE=∠C=90°,
∴DG⊥BF,即DE⊥BF
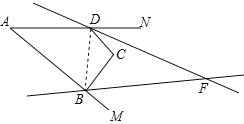
(3)①如图,连接DB,
∵∠A+∠ADC+∠C+∠ABC=360°,∠CDN=180°-∠ADC,∠CBM=180°-∠ABC,
∴∠CDN+∠CBM=∠A+∠C=x+y,
∵BF、DF分别平分∠CBM、∠CDN,
∴∠CDF+∠CBF=![]() (x+y),
(x+y),
∴∠FBD+∠FDB=180°-y+![]() (x+y)=180°-
(x+y)=180°-![]() y+
y+![]() x,
x,
∴∠DFB=180°-(∠FBD+∠FDB)=![]() y-
y-![]() x=30°,
x=30°,
解方程组: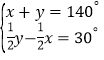 ,
,
解得:![]() ,
,
∴x=40°,y=100°.
②当x=y时,此时∠DFB=0,即∠ABC、∠ADC相邻的外角平分线所在直线互相平行,故当x、y满足x=y时,∠DFB不存在.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
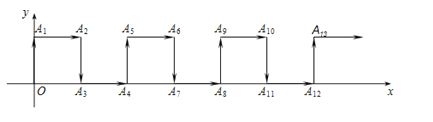
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到![]() (0,1),
(0,1),![]() (1,1),
(1,1),![]() (1,0),
(1,0),![]() (2,0),…那么点
(2,0),…那么点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ ABC 和△ADE都是等边三角形,点 B 在 ED 的延长线上.
(1)求证:△ABD≌△ACE.
(2)求证:AE+CE=BE.
(3)求∠BEC 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
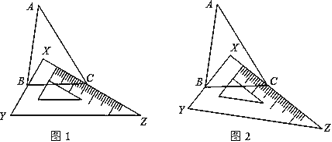
【题目】(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30,则∠ABC+∠ACB=_____,∠XBC+∠XCB=________
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求回答问题:
(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,求线段BE与AF的数量关系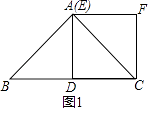
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;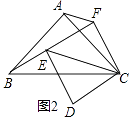
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )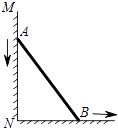
A.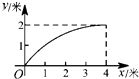
B.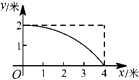
C.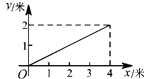
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是( )

A. AB=A′B′=5,BC=B′C′=3 B. AB=B′C′=5,∠A=∠B′=40°
C. AC=A′C′=5,BC=B′C′=3 D. AC=A′C′=5,∠A=∠A′=40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)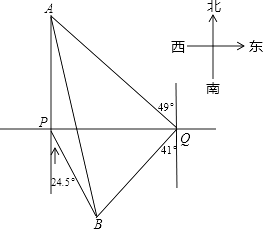
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com