
【题目】如图,△ ABC 和△ADE都是等边三角形,点 B 在 ED 的延长线上.
(1)求证:△ABD≌△ACE.
(2)求证:AE+CE=BE.
(3)求∠BEC 的度数.

【答案】(1)见解析;(2)见解析;(3)∠BEC=60°.
【解析】
(1)由等边三角形的性质可得AB=AC,AD=AE,∠BAC=∠DAE=60°,继而可得∠BAD=∠CAE,利用SAS即可证得△ABD≌△ACE;
(2)由全等三角形的性质可得BD=CE,再由DE=AE即可证得结论;
(3)由等边三角形的性质可得∠ADE=∠AED=60°,从而可得∠ADB=120°,由△ABD≌△ACE ,可得∠AEC=∠ADB=120°,由此即可求得答案.
(1)∵△ ABC 和△ADE 都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE;
(2)∵△ABD≌△ACE,
∴BD=CE,
∵△ADE 是等边三角形,
∴DE=AE,
∵DE+BD=BE,
∴AE+CE=BE;
(3)∵△ADE 是等边三角形,∴∠ADE=∠AED=60°,
∴∠ADB=180°-∠ADE=180°-60°=120°,
∵△ABD≌△ACE ,
∴∠AEC=∠ADB=120°,
∴∠BEC=∠AEC-∠AED=120°-60°=60°.


科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(请在括号里注明重要的推理依据)
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.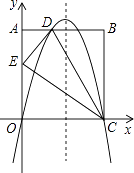
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC∥BD,要使△ABC≌△BAD需再补充一个条件,下列条件中,不能选择的是( )
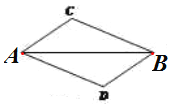
A. BC∥AD B. AC=BD C. BC=AD D. ∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
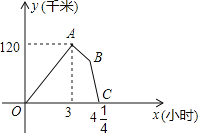
【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
①快递车从甲地到乙地的速度为100千米/时;②甲、乙两地之间的距离为120千米;③图中点B的坐标为(![]() ,75);④快递车从乙地返回时的速度为90千米/时.以上4个结论中正确的是( )
,75);④快递车从乙地返回时的速度为90千米/时.以上4个结论中正确的是( )
A. ①③④ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
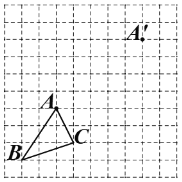
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至![]() 的位置,使点A与
的位置,使点A与![]() 对应,得到△
对应,得到△![]() ;
;
(2)图中可用字母表示,与线段![]() 平行且相等的线有:________;
平行且相等的线有:________;
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=x,∠C=y,(0°<x<180°,0°<y<180°).
(1)∠ABC+∠ADC=_____(用含x、y的代数式表示);
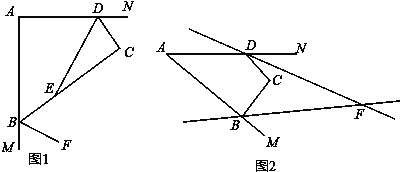
(2)如图1,若x=y=90°,DE平分∠ADC,BF平分与∠ABC相邻的外角,请写出DE与BF的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x<y时,若x+y=140°,∠DFB=30°试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,∠DFB不存在.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com