
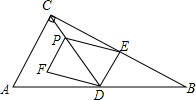
 如图,在△ABC中,∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,D、E分别是边AB、BC的中点,点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作?EDFP,设点P的运动时间为t(秒).
如图,在△ABC中,∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,D、E分别是边AB、BC的中点,点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作?EDFP,设点P的运动时间为t(秒).分析 (1)在RT△ABC中利用勾股定理即可解决问题.
(2)如图1中,当∠DPF=∠PFD时,可以证明PE∥AB,PC=PD,由此即可解决问题.
(3)分两种情形①当0≤t≤$\frac{5}{2}$时,如图2中,作PM⊥DE存在为M,此时重叠部分面积就是平行四边形PEDF的面积,②当$\frac{5}{2}$<t<5时,如图3中,此时y=S△PHD+S△PDE.
(4)两种情形①t=O时,△ADF与△PDE面积相等.②如图4中,当A、P、E共线时△ADF与△PDE面积相等,由DE∥AC得$\frac{DE}{AC}$=$\frac{PD}{PC}$,求出PC即可.
解答 解:(1)在△ABC中,∵∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{(2\sqrt{5})^{2}+(4\sqrt{5})^{2}}$=10. (2)如图1中,∵四边形PEDF是平行四边形,
(2)如图1中,∵四边形PEDF是平行四边形,
∴PF∥DE,PE∥DF,
∴∠DPF=∠PDE,
∵∠ACB=90°,AD=DB,
∴CD=DB=DA=5,∵CE=EB,
∴DE⊥BC,∠CDE=∠EDB
∵∠DPF=∠PFD,
∴∠PED=∠BDE,
∴PE∥DB,∵CE=EB,
∴PC=PD=$\frac{5}{2}$,
∴t=$\frac{5}{2}$.
(3)①当0≤t≤$\frac{5}{2}$时,如图2中,作PM⊥DE存在为M,
∵PM∥CE,
∴$\frac{PM}{CE}$=$\frac{DP}{DC}$,
∴$\frac{PM}{2\sqrt{5}}$=$\frac{5-t}{5}$,
∴PM=$\frac{2\sqrt{5}}{5}$(5-t),
∴Y=DE•PM=$\sqrt{5}$•$\frac{2\sqrt{5}}{5}$(5-t)=-2t+10.
②当$\frac{5}{2}$<t<5时,如图3中, ∵PH∥AC,
∵PH∥AC,
∴$\frac{PH}{AC}$=$\frac{DP}{CD}$,
∴$\frac{PH}{2\sqrt{5}}$=$\frac{5-t}{5}$,
∴PH=$\frac{2\sqrt{5}}{5}$(5-t),
∴y=S△PHD+S△PDE=$\frac{1}{2}$•PH•PM+$\frac{1}{2}$(-2t+10)=$\frac{2}{5}$t2-5t+15,
综上所述:y=$\left\{\begin{array}{l}{-2t+10}&{(0≤t≤\frac{5}{2})}\\{\frac{2}{5}{t}^{2}-5t+15}&{(\frac{5}{2}<t<5)}\end{array}\right.$.
(4)①t=O时,△ADF与△PDE面积相等.
②如图4中,当A、P、E共线时, ∵AE∥DF,△ADF与△PDF同底等高,
∵AE∥DF,△ADF与△PDF同底等高,
∴S△ADF=S△PDF,
∵四边形PFDE是平行四边形,
∴S△PED=S△PDF,
∴S△ADF=S△PDE,
∵DE∥AC,
∴$\frac{DE}{AC}$=$\frac{PD}{PC}$=$\frac{1}{2}$,
∴PC=$\frac{2}{3}$CD=$\frac{10}{3}$,
∴t=$\frac{10}{3}$,
∴t=0或$\frac{10}{3}$时,△ADF与△PDE面积相等.
点评 本题考查四边形综合题,平行四边形的性质、平行线分线段成比例定理,三角形中位线定理等知识,解题的关键是学会分类讨论,正确画出图形,掌握同底等高的三角形面积相等,属于中考常考题型.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
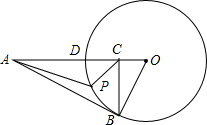 如图,AB切⊙O于B,BC⊥AO于C,AO交⊙O于D,BO=2,AO=8,P是弧BD上任一点,设k=$\frac{PA}{PC}$,问k的值是否随点P的移动而变化?证明你的结论.
如图,AB切⊙O于B,BC⊥AO于C,AO交⊙O于D,BO=2,AO=8,P是弧BD上任一点,设k=$\frac{PA}{PC}$,问k的值是否随点P的移动而变化?证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
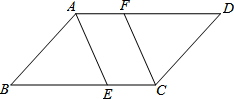 如图:平行四边形ABCD中,(AB≠AD),AE,CF分别平分∠BAD和∠BCD
如图:平行四边形ABCD中,(AB≠AD),AE,CF分别平分∠BAD和∠BCD查看答案和解析>>
科目:初中数学 来源: 题型:填空题
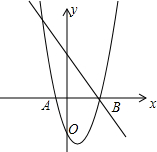 如图,抛物线y=x2-2x-3与x轴交于A、B两点,过B的直线交抛物线于E,且tan∠EBA=$\frac{4}{3}$,有一只蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点处觅食,则蚂蚁从A到E的最短时间是$\frac{64}{9}$s.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,过B的直线交抛物线于E,且tan∠EBA=$\frac{4}{3}$,有一只蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点处觅食,则蚂蚁从A到E的最短时间是$\frac{64}{9}$s.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com