
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像经过点
的图像经过点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
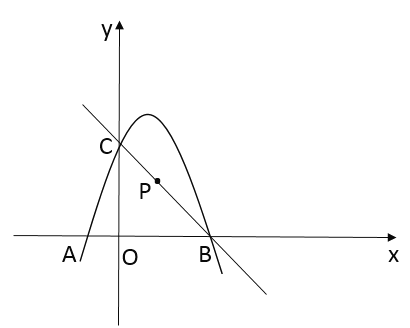
(1)求![]() 、
、![]() 的值:
的值:
(2)若点![]() 为直线
为直线![]() 上一点,点
上一点,点![]() 到直线
到直线![]() 、
、![]() 两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点
两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点![]() ,求新抛物线的顶点坐标.
,求新抛物线的顶点坐标.
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() >0)的图象分别交于点 A(
>0)的图象分别交于点 A(![]() ,4)和点B(8,
,4)和点B(8,![]() ),与坐标轴分别交于点C和点D.
),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当![]() 时,直接写出
时,直接写出![]() 的解集;
的解集;
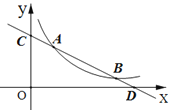
(3)若点P是![]() 轴上一动点,当△COD与△ADP相似时,求点P的坐标.
轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
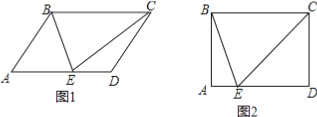
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展了“2020新冠疫情”相关的手抄报竞赛.对于手抄报的主题,组织者提出了两条指导性建议:
(1)A类“武汉加油”、B类“最美逆行者”、C类“万众一心抗击疫情”、D类“如何预防新型冠状病毒”4个中任选一个;
(2)E类为自拟其它与疫情相关的主题.
评奖之余,为了解学生的选题倾向,发掘出最能引发学生触动的主题素材,组织者随机抽取了部分作品进行了统计,并将统计结果绘制成了如下两幅尚不完整的统计图.
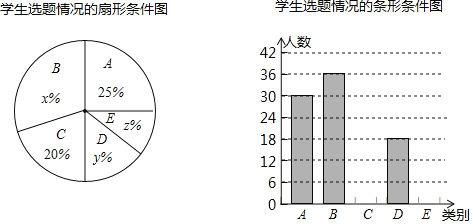
请根据以上信息回答:
(1)本次抽样调查的学生总人数是 ,并补全条形统计图;
(2)扇形统计图中,“C”对应的扇形圆心角的度数是 ,x= ,y﹣z= ;
(3)本次抽样调查中,“学生手抄报选题”最为广泛的是 类.(填字母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克) | 7 | 5 |
价格y(千克) | 2000 | 4000 |
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
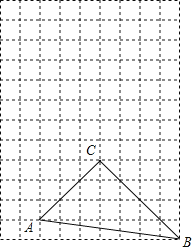
【题目】如图,在每个边长为1的小正方形的网格中,△ABC的顶点A,B,C在格点上,P是BC边上任意一点,以A为中心,取旋转角等于∠BAC,把点P逆时针旋转,点P的对应点为点P',当CP'最短时,画出点P',并说明CP'最短的理由是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
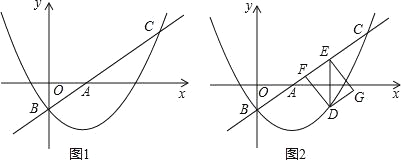
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com