
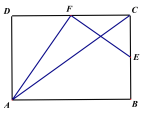
【题目】如图,E、F分别是矩形ABCD的边BC、CD的中点,连接AC、AF、EF,若AF⊥EF,AC=![]() ,则AB的长为_____.
,则AB的长为_____.
【答案】2
【解析】连接BD,由E、F分别BC、CD的中点,得EF=![]() ,设AB=x,则DF=CF=
,设AB=x,则DF=CF=![]() ,由勾股定理得,CE2+CF2=EF2 ,求得
,由勾股定理得,CE2+CF2=EF2 ,求得![]() ,AD=2CE=
,AD=2CE=![]() ,再证△ADF∽△FCE,得
,再证△ADF∽△FCE,得![]() ,即
,即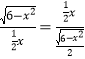 ,化简可得.
,化简可得.
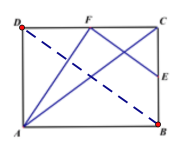
连接BD,
因为,四边形ABCD是矩形,
所以,BD=AC=![]() ,
,
因为,E、F分别BC、CD的中点,
所以,EF=![]() ,
,
设AB=x,则DF=CF=![]() ,
,
由勾股定理得,CE2+CF2=EF2 ,
即![]() ,
,
![]() ,
,
所以,AD=2CE=![]() ,
,
因为,EF⊥AF,
所以,∠AFE=90o
所以,∠AFD+∠CFE=90o
又因为,∠CEF+∠CFE=90o
所以,∠AFD=∠CEF
又∠ADF=∠FCE==90o
所以,△ADF∽△FCE
所以,![]()
所以,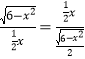
解得x=2.
即AB=2.
故答案为:2


科目:初中数学 来源: 题型:
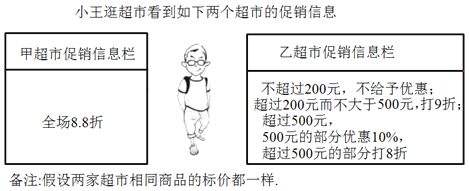
【题目】(1)当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
门头沟盛产名特果品,东山的京白梨,灵水的核桃,柏峪的扁杏仁,龙泉雾的香白杏,火村红杏,太子墓的红富士苹果,陇驾庄盖柿都是上等的干鲜果品,有的曾为皇宫供品,至今在国内享有盛名.秋收季节,某公司打算到门头沟果园基地购买一批优质苹果.果园基地对购买量在1000千克(含1000千克)以上的有两种销售方案,方案一:每千克10元,由基地送货上门;方案二:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5000元.
(1)公司购买多少千克苹果时,选择两种购买方案的付款费用相同;
(2)如果公司打算购买3000千克苹果,选择哪种方案付款最少?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG. 
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E. 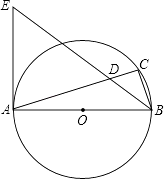
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题: 
(1)抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.
(2)若学校有600名学生,请估计该校训练后成绩为“A”等次的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:AC2=APAB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com