
【题目】(1)当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?
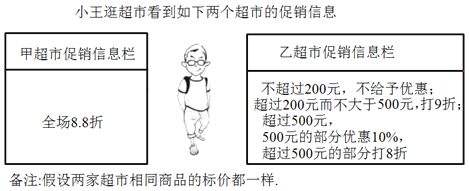
【答案】(1)当一次性购物标价总额是300元时, 甲超市实付款264(元), 乙超市实付款270(元);
(2)当标价总额是625元时,甲、乙超市实付款一样; (3)若他只去一次该超市购买同样多的商品,可以节省39.6或22元.
【解析】
试题(1)根据两家超市的优惠方案,可知当一次性购物标价总额是300元时,甲超市付款=购物标价×0.88,乙超市付款=300×0.9,分别计算即可得;
(2)设当标价总额是x元时,甲、乙超市实付款一样,根据甲超市实付款=乙超市实付款列出方程,求解即可;
(3)首先计算出两次购物标价,然后根据优惠方案即可求解.
试题解析:(1)当一次性购物标价总额是300元时,
甲超市实付款=300×0.88=264(元),
乙超市实付款=300×0.9=270(元);
(2)设当标价总额是x元时,甲、乙超市实付款一样.
当一次性购物标价总额是500元时,
甲超市实付款=500×0.88=440(元),乙超市实付款=500×0.9=450(元),
∵440<450, ∴x>500.
根据题意得0.88x=500×0.9+0.8(x-500),
解得x=625,
答:当标价总额是625元时,甲、乙超市实付款一样;
(3)小王两次到乙超市分别购物付款198元和466元,
第一次购物付款198元,购物标价可能是198元,也可能是198÷0.9=220元,
第二次购物付款466元,购物标价是(466-450)÷0.8+500=520元,
两次购物标价之后是198+520=718元,或220+520=740元,
若他只去一次该超市购买同样多的商品,实付款500×0.9+0.8(718-500)=624.4元,或500×0.9+0.8(740-500)=642元,
可以节省198+466-624.4=39.6元,或198+466-642=22元,
答:若他只去一次该超市购买同样多的商品,可以节省39.6或22元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+bx+c的图象与x轴交于两点,与y轴的正半轴交于一点,且对称轴为x=1,则下列说法正确的是( )
A.二次函数的图象与x轴的交点位于y轴的两侧
B.二次函数的图象与x轴的交点位于y轴的右侧
C.其中二次函数中的c>1
D.二次函数的图象与x轴的一个交于位于x=2的右侧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
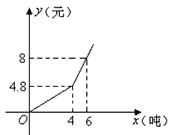
(1)分别求出当0≤x≤4、x>4时函数的解析式;
(2)当0≤x≤4、x>4时,每吨水的价格分别是多少?
(3)若某用户该月交水费12.8元,求该户用了多少吨水.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满足_________条件时,四边形BEDF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5 ![]() 千米的C处.
千米的C处.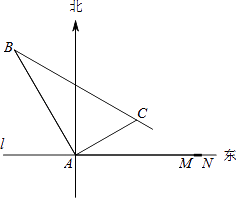
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
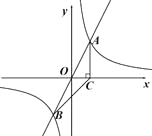
(1)求反比例函数的解析式;
(2)若点P是反比例函数![]() 图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,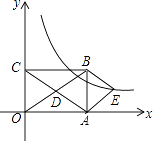
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com