
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
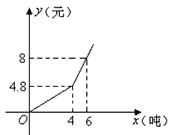
(1)分别求出当0≤x≤4、x>4时函数的解析式;
(2)当0≤x≤4、x>4时,每吨水的价格分别是多少?
(3)若某用户该月交水费12.8元,求该户用了多少吨水.
【答案】(1)y=1.2x(0≤x≤4),y=1.6x-1.6(x>4);(2)1.2元/吨;1.6元/吨(3) 9吨.
【解析】试题分析:(1)仔细观察图象,便可写出函数在不同范围内的函数解析式;
(2)根据在不同范围内的函数的解析式可知,在0﹣4吨范围内,每吨1.2元,当x>4时,每吨水1.6元;
(3)根据已知条件可知:该用户的交水费范围属于x>4的范围,代入解析式即可得到答案.
试题解析:解:(1)当0≤x≤4时,设y=k1x,把点(4,4.8)代入y=k1x得k1=1.2,得y=1.2x;
当x>4时,设y=k2x+b,把点(4,4.8)和(6,8)代入y=k2x+b得k2=1.6,b=﹣1.6,
得y=1.6x﹣1.6;
(2)根据(1)中得到的函数的解析式可知:
当0≤x≤4时,每吨水1.2元;
当x>4时,当x=5,1.6x﹣1.6=6.4,当x=4,y=4.8,则每吨水1.6元;
(3)把y=12.8代入y=1.6x﹣1.6中得:x=9.
答:他用了9吨水.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】某公路上一路段的道路维修工程准备对外招标,现有甲、乙两个工程队竞标,竞标资料上显示:甲工程队单独完成此项工程需要10天,乙工程队单独完成此项工程需要15天,但甲工程队每天的工程费用比乙工程队多300元;甲、乙两队合作共需要10200元.工程指挥队决定从甲、乙两个工程队中选一队单独完成,若从节省资金的角度考虑,应选哪个工程队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
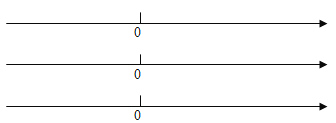
(1)点A表示的数为 ,点B表示的数为 ,点C表示的数为 .
(2)用含t的代数式表示P到点A和点C的距离: PA= ,PC= .
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.①在点Q向点C运动过程中,能否追上点P?若能,请求出点Q运动几秒追上.②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A.m≤2或m≥3
B.m≤3或m≥4
C.2<m<3
D.3<m<4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①最大的负整数是﹣1;②|a|=a;③a+5一定比a大;④38万用科学记数法表示为38×104;⑤单项式﹣![]() 的系数是﹣2,次数是3;⑥﹣
的系数是﹣2,次数是3;⑥﹣![]() <﹣
<﹣![]() ;⑦长方体的截面中,边数最多的多边形是七边形.
;⑦长方体的截面中,边数最多的多边形是七边形.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
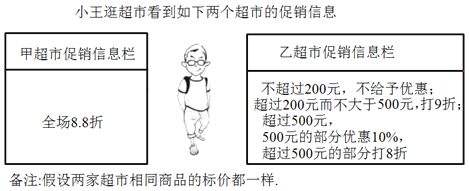
【题目】(1)当一次性购物标价总额是300元时,甲、乙超市实付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,则下列说法:①MN=HC;②MH=![]() (AH﹣HB);③MN=
(AH﹣HB);③MN=![]() (AC+HB);④HN=
(AC+HB);④HN=![]() (HC+HB),其中正确的是( )
(HC+HB),其中正确的是( )
![]()
A.①② B.①②④ C.②③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG. 
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com