
【题目】如图,矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°,CF⊥BD于F.下列结论:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正确的结论有( )
AO,④CE=CF.正确的结论有( )
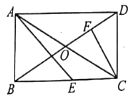
A. ①②B. ②③C. ①②④D. ①②③
【答案】D
【解析】
根据矩形的性质,由∠ADB=30°可得,△AOB和△COD都是等边三角形,再由∠AEB=45°,可得△ABE是等腰直角三角形,其边有特殊的关系,利用等量代换可以得出③AE=![]() AO是正确的,①BE=CD是正确的,在正△COD中,CF⊥BD,可得DF=
AO是正确的,①BE=CD是正确的,在正△COD中,CF⊥BD,可得DF=![]() CD,再利用等量代换可得②BF=3DF是正确的,利用选项的排除法确定选项D是正确的.
CD,再利用等量代换可得②BF=3DF是正确的,利用选项的排除法确定选项D是正确的.
解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AC=BD,AO=CO=BO=DO,∠ABC=∠ADC=∠BAD=∠BCD=90°,
∵∠AEB=45°,
∴∠BAE=∠AEB=45°
∴AB=BE=CD,AE=![]() AB=
AB=![]() CD,
CD,
故①正确,
∵∠ADB=30°,
∴∠ABO=60°且AO=BO,
∴△ABO是等边三角形,
∴AB=AO,
∴AE=![]() AO,
AO,
故③正确,
∵△OCD是等边三角形,CF⊥BD,
∴DF=FO=![]() OD=
OD=![]() CD=
CD=![]() BD,
BD,
∴BF=3DF,
故②正确,
根据排除法,可得选项D正确,
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】综合与探究
阅读理解:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如:
在数轴上,有理数3与1对应的两点之间的距离为![]() ;
;
在数轴上,有理数3与-2对应的两点之间的距离为![]() ;
;
在数轴上,有理数-3与-2对应的两点之间的距离为![]() .
.
解决问题:如图所示,已知点![]() 表示的数为-3,点
表示的数为-3,点![]() 表示的数为-1,点
表示的数为-1,点![]() 表示的数为2.
表示的数为2.
![]()
(1)点![]() 和点
和点![]() 之间的距离为______.
之间的距离为______.
(2)若数轴上动点![]() 表示的数为
表示的数为![]() ,当
,当![]() 时,点
时,点![]() 和点
和点![]() 之间的距离可表示为______;当
之间的距离可表示为______;当![]() 时,点
时,点![]() 和点
和点![]() 之间的距离可表示为______.
之间的距离可表示为______.
(3)若数轴上动点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在点
在点![]() 和点
和点![]() 之间,点
之间,点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() (用含
(用含![]() 的代数式表示并进行化简)
的代数式表示并进行化简)
(4)若数轴上动点![]() 表示的数为-2,将点
表示的数为-2,将点![]() 向右移动19个单位长度,再向左移动23个单位长度终点为
向右移动19个单位长度,再向左移动23个单位长度终点为![]() ,那么
,那么![]() ,
,![]() 两点之间的距离是______.
两点之间的距离是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)求出该反比例函数解析式;
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() ,顶点为
,顶点为![]() .
.
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?如果存在,求出点
为直角三角形?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
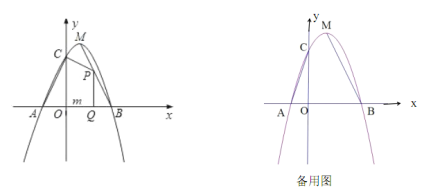
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图平面直角坐标系中,O(0,0),A(4,4![]() ),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(8,0).将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则CE:DE的值是 .
,则CE:DE的值是 .
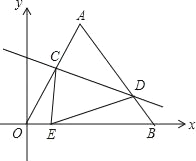
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=![]() .
.
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.
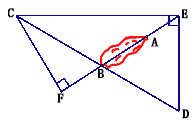
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).
(1)观察一个等比列数1,![]() ,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:
令S=1+2+4+8+16+…+230…①
等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②
由② ﹣ ①式,得2S﹣S=231﹣1
即(2﹣1)S=231﹣1
所以 ![]()
请根据以上的解答过程,求3+32+33+…+323的值;
(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示an;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+an.
查看答案和解析>>
科目:初中数学 来源: 题型:
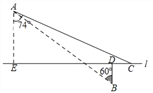
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com