
【题目】完成下面的证明(下划线内补全证明过程,括号内填写推理的依据).
(1)如图1,AB∥CD,∠B+∠D=180°,求证:CB∥DE 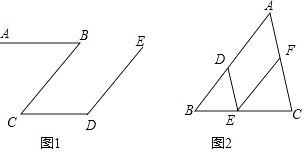
证明:∵AB∥CD(已知)
∴∠B=
∵∠B+∠D=180°(已知)
∴∠C+∠D=180°(等量代换)
∴∥
(2)如图2,已知DE∥AC,∠A=∠DEF,请证明∠B=∠FEC. 证明:∵DE∥AC(已知)
∴∠A=
∵∠A=∠DEF(已知)
∴∠DEF=∠(等量代换)
∴AB∥
∴∠=∠ .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有一个周长为80cm的正方形,从四个角各减去一个正方形,做成一个无盖盒子。设这个盒子的底面面积为y cm,减去的正方形的边长为x cm,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x﹣(k+1)与双曲线y= ![]() 相交于B、C两点,与x轴相交于A点,BM⊥x轴交x轴于点M,S△OMB=
相交于B、C两点,与x轴相交于A点,BM⊥x轴交x轴于点M,S△OMB= ![]()
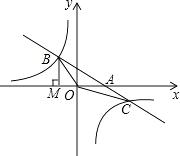
(1)求这两个函数的解析式;
(2)若已知点C的横坐标为3,求A、C两点坐标;
(3)在(2)条件下,是否存在点P,使以A、O、C、P为顶点的四边形是平行四边形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多项式m(n-2)-m2(2-n)因式分解等于( )
A. (n-2)(m+m2) B. (n-2)(m-m2)
C. m(n-2)(m+1) D. m(n-2)(m-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个. 1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.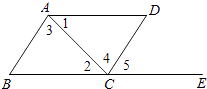
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com