
【题目】如图所示,直线AB交x轴于点A(![]() ,0),交y轴于点B(0,
,0),交y轴于点B(0,![]() ),且
),且![]() .b满足
.b满足![]()
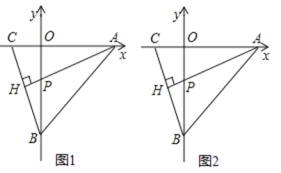
(1)求证:OA=OB;
(2)如图1,若C的坐标为(-1,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;
(3)如图2,连接OH,求证:∠OHP=45°.
【答案】(1)详见解析;(2)点P坐标为(0,-1);(3)详见解析.
【解析】
(1)通过非负性先求出a和b的值,进而即可得解;
(2)通过证明![]() ,得到OP=OC=1,进而即可得解;
,得到OP=OC=1,进而即可得解;
(3)过点O分别作OM⊥CB于点M,作ON⊥HA于点N,通过证明![]() ,
,![]() 进行求解即可.
进行求解即可.
(1)证明:∵![]() ,且
,且![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴OA=OB=4;
(2)解:∵AH⊥BC于H,
∴∠OAP+∠OPA=∠BPH+∠OBC=90°,
∵∠OPA=∠BPH
∴∠OAP=∠OBC
∵∠COB=∠POA=90°,OA=OB
∴![]()
∴OP=OC=1
∴点P坐标为![]() ;
;
(3)解:如下图,过点O分别作OM⊥CB于点M,作ON⊥HA于点N,连接OH.
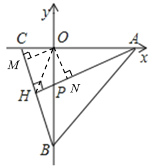
∴![]()
∵∠OAP=∠OBC,OB=OA
∴![]()
∴OM=ON
∵OH=OH
∴![]()
∴∠OHM=∠OHN
∵![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为( )
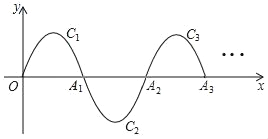
A. 4 B. ﹣4 C. ﹣6 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形OABC的顶点O在坐标原点,顶点A,C在反比例函数y=![]() 的图象上,点A的横坐标为4,点B的横坐标为6,且平行四边形OABC的面积为9,则k的值为_____.
的图象上,点A的横坐标为4,点B的横坐标为6,且平行四边形OABC的面积为9,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
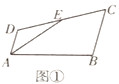
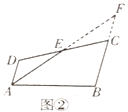
【题目】在数学活动课上,数学老师出示了如下题目:
如图①,在四边形![]() 中,
中,![]() 是边
是边![]() 的中点,
的中点,![]() 是
是![]() 的平分线,
的平分线,![]() .
.
求证:![]() .
.
小聪同学发现以下两种方法:
方法1:如图②,延长![]() 、
、![]() 交于点
交于点![]() .
.
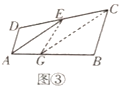
方法2:如图③,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() .
.
(1)请你任选一种方法写出这道题的完整的证明过程;
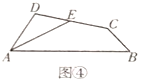
(2)如图④,在四边形![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
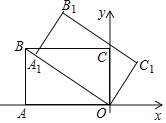
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
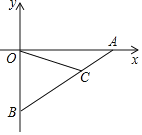
【题目】在平面直角坐标系中点![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点且
轴上的点且![]() 点的坐标是
点的坐标是![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上,是靠近点
上,是靠近点![]() 的三等分点.点
的三等分点.点![]() 是
是![]() 轴上的点,当
轴上的点,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
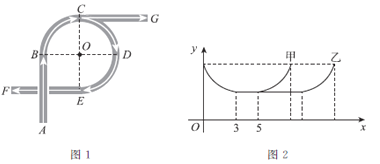
【题目】如图1是一座立交桥的示意图(道路宽度忽略不计), A为入口, F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF ;弯道为以点O为圆心的一段弧,且![]() ,
,![]() ,
,![]() 所对的圆心角
所对的圆心角![]() 均为90°.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出. 其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法:①甲车在立交桥上共行驶8s;②从F口出比从G口出多行驶40m;③甲车从F口出,乙车从G口出;④立交桥总长为150m.其中正确的是( )
均为90°.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出. 其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法:①甲车在立交桥上共行驶8s;②从F口出比从G口出多行驶40m;③甲车从F口出,乙车从G口出;④立交桥总长为150m.其中正确的是( )
A. ①②③ B. ①②④ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
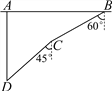
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com