
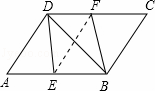
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.

(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,
∵E、F分别为边AB、CD的中点,
∴AE=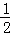 AB,CF=
AB,CF=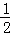 CD,
CD,
∴AE=CF,
在△ADE和△CBF中,
∵
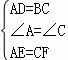 ,
,
∴△ADE≌△CBF(SAS);
(2)若∠ADB是直角,则四边形BEDF是菱形,理由如下:
解:由(1)可得BE=DF,
又∵AB∥CD,
∴BE∥DF,BE=DF,
∴四边形BEDF是平行四 边形,
边形,
连接EF,在▱ABCD中,E、F分别为边AB、CD的中点,
∴DF∥AE,DF=AE,
∴四边形AEFD是平行四边形,
∴EF∥AD,
∵∠ADB是直角,
∴AD⊥BD,
∴EF⊥BD,
又∵四边形BFDE是平行四边形,
∴四边形BFDE是菱形.
点评: 本题主要考查了平行四边形的性质,全等三角形的判定以及菱形的判定,利用好E、F是中点是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
学校要组织足球比赛.赛制为单循环形式(每两队之间赛一场).计划安排21场比赛,应邀请多少个球队参赛?设邀请x个球队参赛.根据题意,下面所列方程正确的是( )
A. x2=21 B.  x(x﹣1)=21 C.
x(x﹣1)=21 C.  x2=21 D. x(x﹣1)=21
x2=21 D. x(x﹣1)=21
查看答案和解析>>
科目:初中数学 来源: 题型:
将图1的正方形作如下操作:第1次分别连接对边中点如图2,得到5个正方形;第2次将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,第n次操作后,得到正方形的个数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF=( )

A.  B. 2
B. 2 C. 3 D. 3
C. 3 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
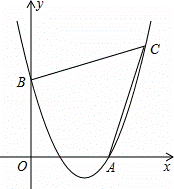
)如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的▱DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边 形AOBC的顶点重合)若能,求出▱DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
形AOBC的顶点重合)若能,求出▱DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com