
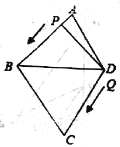
【题目】如图,四边形![]() 的三边(
的三边(![]() 、
、![]() 、
、![]() )和
)和![]() 的长度都为5厘米,动点
的长度都为5厘米,动点![]() 从
从![]() 出发
出发![]() 到
到![]() ,速度为2厘米/秒,动点
,速度为2厘米/秒,动点![]() 从点
从点![]() 出发
出发![]() 到
到![]() .速度为
.速度为![]() 厘米/秒.5秒后
厘米/秒.5秒后![]() 、
、![]() 相距3厘米,试确定5秒时
相距3厘米,试确定5秒时![]() 的形状.
的形状.
【答案】直角三角形
【解析】
首先根据题意确定出5秒时P、Q的位置,然后进一步利用勾股定理的逆定理证明出△BPQ为直角三角形,据此进一步证明出△APQ为直角三角形即可.
∵AB=BD=5(厘米),动点![]() 从
从![]() 出发
出发![]() 到
到![]() ,速度为2厘米/秒,
,速度为2厘米/秒,
∴5秒时,P点的运动路程为:![]() (厘米),
(厘米),
∵AB+BD=10(厘米),
∴此时P点与D点重合,
∵AB=BC=CD=5(厘米),动点![]() 从点
从点![]() 出发
出发![]() 到
到![]() .速度为
.速度为![]() 厘米/秒,
厘米/秒,
∴5秒时,Q点的运动路程为:![]() (厘米),
(厘米),
∵DC+CB+BA=15(厘米),
∴此时点Q在AB边上,且BQ=4(厘米),
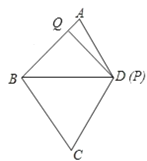
如图,在△BPQ中,
∵BQ=4(厘米),PQ=3(厘米),BP=5(厘米),
∴![]() ,
,
∴△BPQ为直角三角形,∠BQP=90°,
∴∠AQP=180°∠BQP=90°,
∴△APQ为直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
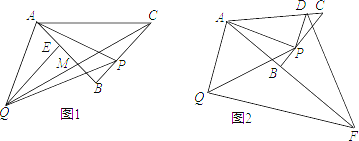
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
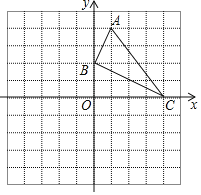
【题目】如图,已知网格上最小的正方形的边长为![]() (长度单位),点
(长度单位),点![]() 在格点上.
在格点上.
(1)直接在平面直角坐标系中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() (点
(点![]() 对应点
对应点![]() ,点
,点![]() 对应点
对应点![]() );
);
(2)![]() 的面积为 (面积单位)(直接填空);
的面积为 (面积单位)(直接填空);
(3)点![]() 到直线
到直线![]() 的距离为 (长度单位)(直接填空);
的距离为 (长度单位)(直接填空);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13 个结,然后以3个结间距、4 个结间距、5 个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
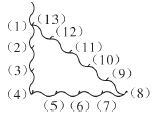
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.三角形两条短边的平方和等于长边的平方
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=2x﹣2与x轴交于点A1,如图所示,依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnnCn﹣1,使得点A1,A2,A3,…An在直线l上,点C1,C2,C3,…n在y轴正半轴上,则正方形AnBnnCn﹣1的面积是_____.
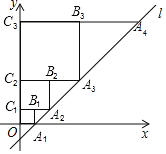
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则下列式子中①abc<0;②0<b<-2a;③![]() ; ④a+b+c<0成立的个数有( )
; ④a+b+c<0成立的个数有( )
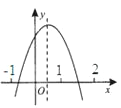
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形![]() 中,
中,![]() ,对角线
,对角线![]() 于
于![]() 点,点
点,点![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 在
在![]() 轴上.
轴上.
![]() 若
若![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 若
若![]() ,
,![]() ,求过
,求过![]() 点的反比例函数的解析式;
点的反比例函数的解析式;
![]() 如图,在
如图,在![]() 上有一点
上有一点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,在
,在![]() 上取
上取![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,(不与
上运动时,(不与![]() 、
、![]() 重合),
重合),![]() 的值是否发生变化?若变化,求出变化范围;若不变,求出其值.
的值是否发生变化?若变化,求出变化范围;若不变,求出其值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com