【题目】计算（每小题4分，共16分）
（1）
（2）已知
．求代数式
的值.
（3）先化简，再求值
，其中
.
（4）解分式方程：
+3．
【答案】（1）1；（2）7；（3）
；（4）
【解析】
（1）根据幂的乘方、平方差公式、去绝对值解决即可.
（2）根据整式乘法法则，将原式变形成2a2+3a+1，再将
变形成2a2+3a=6，代入计算即可.
（3）根据分式的基本性质，先将原式化简成
，将m的值代入计算即可.
（4）根据等式和分式的基本性质，将分式方程化简成整式方程求解即可.
（1）
，
；
，
，
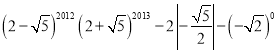=1.
（2）解：原式=6a2+3a-（4a2-1）
=6a2+3a-4a2+1
=2a2+3a+1
∵2a2+3a-6=0
2a2+3a=6
原式=6+1=7
（3）
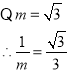
（4）
方程两边都乘以
得：
解得：
检验：当
时，2（x﹣1）≠0，
所以是原方程的解，
即原方程的解为.
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】现有甲、乙两个空调安装队分别为A、B两个公司安装空调，甲安装队为A公司安装66台空调，乙安装队为B公司安装80台空调，乙安装队提前一天开工，最后与甲安装队恰好同时完成安装任务．已知甲队比乙队平均每天多安装2台空调，求甲、乙两个安装队平均每天各安装多少台空调．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将直角三角形分割成一个正方形和两对全等的直角三角形，在
中，
，
，
，
；在正方形
中，
.
探究1
（1）小明发现了求正方形边长的方法：由题意可得
，
，因为
，所以
，解得
探究2
（2）小亮发现了另一种求正方形边长的方法：连接
，利用
可以得到
与
的关系.请根据小亮的思路完成他的求解过程.
探究3
（3）请结合小明和小亮得到的结论验证勾股定理.（注：根据比例的基本性质，由
可得
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一元二次方程x2+kx﹣3＝0的一个根是x＝1，则另一个根是___．
【答案】-3．
【解析】
解：∵x=1是一元二次方程的根，∴12+k×1-3=0，∴k=2，∴x2+2x-3=0，∴（x+3）（x-1）=0，∴x1=-3，x2=1．故答案为：-3．
【题型】填空题
【结束】
19
【题目】如图，在△ABC中，AB=8，AC=6，AD=12，点D在BC的延长线上，且△ACD∽△BAD，求BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
是等腰直角三角形，
，点
是
的中点，延长
至点
，使
，连接
（如图①）.
（1）求证：
≌
；
（2）已知点
是
的中点，连接
（如图②）.
①求证: ≌
；
②如图③，延长
至点
，使
，连接
，求证：
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=﹣x+1与x轴，y轴分别交于B，A两点，动点P在线段AB上移动，以P为顶点作∠OPQ=45°交x轴于点Q．
（1）求点A和点B的坐标；
（2）比较∠AOP与∠BPQ的大小，说明理由．
（3）是否存在点P，使得△OPQ是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
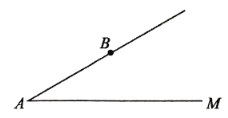
【题目】（1）如图，
，
.点
在射线
上，利用图，画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题.你画图时，选取的
的长约为__________
（精确到0.1）.
（2）
为锐角，
，点在射线上，点
到射线的距离为
，
，若
的形状、大小是唯一确定的，则
的取值范围是__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC，PB：PC=1：2．
（1）求证：AC平分∠BAD；
（2）探究线段PB，AB之间的数量关系，并说明理由；
（3）若AD=3，求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
