
【题目】已知∠AOB=90°,∠COD=30°.
(1)如图1,当点O、A、C在同一条直线上时,∠BOD的度数是;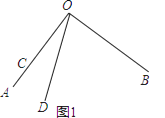
(2)将∠COD从图1的位置开始,绕点O逆时针方向旋转n°(即∠AOC=n°),且0<n<180.
①如果∠COD的一边与∠AOB的一边垂直,则n= .
②当60<n<90时(如图2),作射线OM平分∠AOC,射线ON平分∠BOD,试求∠MON的度数 . 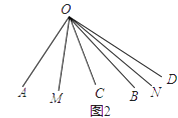
【答案】
(1)60°
(2)60、90、150,60°
【解析】解:(1)∠BOD=∠AOB﹣∠AOD=∠AOB﹣∠COD=90°﹣30°=60°.
故答案为:60°.(2)①∵0<n<180,
∴分三种情况.
a:点D在射线0B上,∠AOC=∠AOB﹣∠COD=90°﹣30°=60°;
b:点C在射线OB上,∠AOC=∠AOB=90°;
c:点D在AO的延长线上,∠AOC=180°﹣∠COD=180°﹣30°=150°.
综上得n为60、90、150.
故答案为:60、90、150.②∵∠AOC=n°,OM平分∠AOC,
∴∠AOM= ![]() n°,
n°,
∠AOD=∠AOC+∠COD=n°+30°,
∠BOD=∠AOD﹣∠AOB=n°+30°﹣90°=n°﹣60°,
∵ON平分∠BOD,
∴∠DON= ![]() ∠BOD=
∠BOD= ![]() ×(n°﹣60°)=
×(n°﹣60°)= ![]() n°﹣30°,
n°﹣30°,
∠MON=∠AOD﹣∠AOM﹣∠DON=n°+30°﹣ ![]() n°﹣(
n°﹣( ![]() n°﹣30°)=60°
n°﹣30°)=60°
(1)根据,∠BOD=∠AOB﹣∠AOD=∠AOB﹣∠COD,而∠AOD=∠COD=30°,代入即可求出结论;
(2)①0<n<180,在旋转的过程中,能够发现∠COD的一边与∠AOB的一边垂直共有三种情况,分别求出每种情况下旋转的度数即可;
②∠AOC=n°,OM平分∠AOC,根据角平分线的定义及角与角之间的关系,将直接求∠MON得度数转换成求∠AOM,∠DON的度数,再依照角的关系即可求得结论.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】规定一种新运算:a*b=a+b,ab=a﹣b,其中a、b为有理数,如a=2,b=1时,a*b=2+1=3,ab=2﹣1=1根据以上的运算法则化简:a2b*3ab+5a2b4ab,并求出当a=5,b=3时多项式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
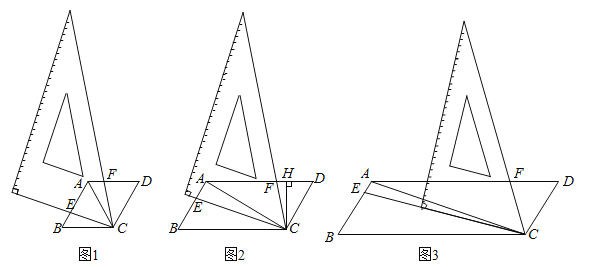
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:![]() 的值为常数t,则t= .
的值为常数t,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的边OB上的一点.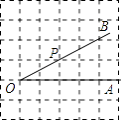
(1)过点P画OB的垂线,交OA于点C,
(2)过点P画OA的垂线,垂足为H,
(3)线段PH的长度是点P到的距离,线段是点C到直线OB的距离.
(4)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是(用“<”号连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,中国水资源总量约为27500亿立方米,居世界第六位,其中数据27500亿用科学记数法表示为( )
A.2.75×108
B.2.75×1012
C.27.5×1013
D.0.275×1013
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com