
【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F. 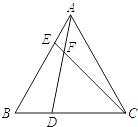
(1)求证:AD=CE;
(2)求∠DFC的度数.
科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,∠COD=30°.
(1)如图1,当点O、A、C在同一条直线上时,∠BOD的度数是;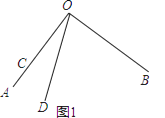
(2)将∠COD从图1的位置开始,绕点O逆时针方向旋转n°(即∠AOC=n°),且0<n<180.
①如果∠COD的一边与∠AOB的一边垂直,则n= .
②当60<n<90时(如图2),作射线OM平分∠AOC,射线ON平分∠BOD,试求∠MON的度数 . 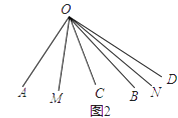
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,![]() =3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证:![]() ;
;
(2)若∠CGF=90°,求![]() 的值.
的值.
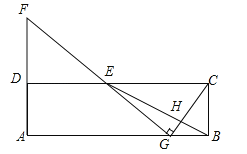
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国某部边防军小分队成一列在野外行军,通讯员在队伍中,数了一下他前后的人数,发现前面人数是后面的两倍,他往前超了6位战士,发现前面的人数和后面的人数一样.
(1)这列队伍一共有多少名战士?
(2)这列队伍要过一座320米的大桥,为安全起见,相邻两个战士保持相同的一定间距,行军速度为5米/秒,从第一位战士刚上桥到全体通过大桥用了100秒时间,请问相邻两个战士间距离为多少米(不考虑战士身材的大小)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠A的两边与∠B的两边分别平行,且∠A的度数比∠B的度数的3倍少40°,则∠B的度数为( )
A. 20° B. 55° C. 20°或55° D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com